Overview

Machine learning is the field that teaches machines and computers to learn from existing data to make predictions on new data: Will a tumor be benign or malignant? Which of your customers will take their business elsewhere? Is a particular email spam? We will use Python to perform supervised learning, an essential component of machine learning. We will build predictive models, tune their parameters, and determine how well they will perform with unseen data—all while using real world datasets. We be using scikit-learn, one of the most popular and user-friendly machine learning libraries for Python.

Libraries

from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import (train_test_split,
                                     cross_val_score,
                                     GridSearchCV,
                                     RandomizedSearchCV)
from sklearn.linear_model import (LinearRegression, 
                                  Ridge, 
                                  Lasso, 
                                  LogisticRegression, 
                                  ElasticNet)
from sklearn.metrics import (mean_squared_error, 
                             classification_report, 
                             confusion_matrix, 
                             roc_curve,
                             roc_auc_score,
                             precision_recall_curve,
                             plot_precision_recall_curve)
from sklearn.tree import DecisionTreeClassifier
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC # Support Vector Classiffication
from sklearn.preprocessing import (scale, StandardScaler)

import pandas as pd
import numpy as np
from scipy.stats import randint

import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline

import warnings
warnings.filterwarnings("ignore")

plt.style.use("ggplot")

Classification

Introduction to classification problems and how to solve them using supervised learning techniques. We’ll explore a political dataset, where we will classify the party affiliation of United States congressmen based on their voting records.

Supervised learning

What is machine learning?

The art and science of:

Giving computers the ability to learn to make decisions from data

without being explicitly programmed!

Examples:

Learning to predict whether an email is spam or not

Clustering wikipedia entries into different categories

Supervised learning: Uses labeled data

Unsupervised learning: Uses unlabeled data

Unsupervised learning

Uncovering hidden patterns from unlabeled data

Example:

Grouping customers into distinct categories (Clustering)

Reinforcement learning

Software agents interact with an environment

Learn how to optimize their behavior

Given a system of rewards and punishments

Draws inspiration from behavioral psychology

Applications

Economics

Genetics

Game playing

AlphaGo: First computer to defeat the world champion in Go

Supervised learning

Predictor variables/features and a target variable

Aim:

Predict the target variable, given the predictor variables

Classication: Target variable consists of categories

Regression: Target variable is continuous

Naming conventions

Features = predictor variables = independent variables

Target variable = dependent variable = response variable

Supervised learning

Automate time-consuming or expensive manual tasks

Example: Doctor’s diagnosis

Make predictions about the future

Example: Will a customer click on an ad or not?

Need labeled data

Historical data with labels

Experiments to get labeled data

Crowd-sourcing labeled data

Supervised learning in Python

We will use scikit-learn/sklearn

Integrates well with the SciPy stack

Otherlibraries

Tensor Flow

keras

Exploratory data analysis

The Iris dataset

Features:

Petal length

Petal width

Sepal length

Sepal width

Target variable:

Species Versicolor

Virginica

Setosa

The Iris dataset in scikit-learn

iris = datasets.load_iris()
type(iris)

sklearn.utils.Bunch

iris.keys()

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])

type(iris.data)

numpy.ndarray

type(iris.target)

numpy.ndarray

iris.data.shape

(150, 4)

iris.target_names

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

Exploratory data analysis (EDA)

X = iris.data
y= iris.target
df = pd.DataFrame(X, columns=iris.feature_names)
df.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

df2 = df.copy()
df2['target_names'] = iris.target
df2.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

iris.target_names

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

df2.target_names.value_counts()

2    50
1    50
0    50
Name: target_names, dtype: int64

df2['target_names'] = df2.target_names.map({0:'setosa', 1:'versicolor', 2:'virginica'})
df2.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target_names
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa

Visual EDA

_ = pd.plotting.scatter_matrix(df, c=y, figsize=[8,8], s=150, marker="D")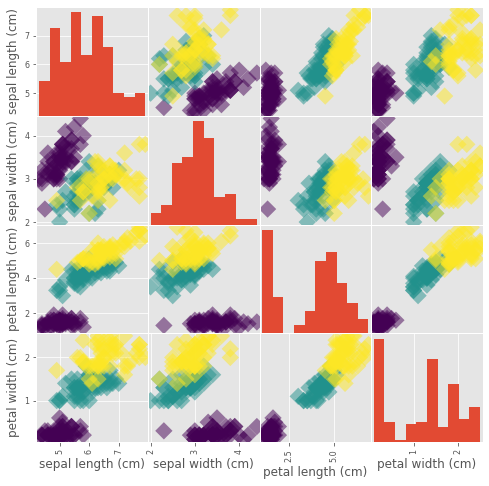

Numerical EDA

We’ll be working with a dataset obtained from the UCI Machine Learning Repository consisting of votes made by US House of Representatives Congressmen. our goal will be to predict their party affiliation (‘Democrat’ or ‘Republican’) based on how they voted on certain key issues.

Note

Here, it’s worth noting that we have preprocessed this dataset to deal with missing values. This is so that our focus can be directed towards understanding how to train and evaluate supervised learning models.

Before thinking about what supervised learning models we can apply to this, however, we need to perform Exploratory data analysis (EDA) in order to understand the structure of the data.

votes = pd.read_csv("datasets/votes.csv")
votes.head()

	party	infants	water	budget	physician	salvador	religious	immigration	synfuels	education	superfund	crime	duty_free_exports	eaa_rsa
0	republican	0	1	0	1	1	1	1	0	1	1	1	0	1
1	republican	0	1	0	1	1	1	0	0	1	1	1	0	1
2	democrat	0	1	1	0	1	1	0	1	0	1	1	0	0
3	democrat	0	1	1	0	1	1	0	1	0	1	0	0	1
4	democrat	1	1	1	0	1	1	0	1	0	1	1	1	1

votes.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 435 entries, 0 to 434
Data columns (total 17 columns):
 #   Column             Non-Null Count  Dtype 
---  ------             --------------  ----- 
 0   party              435 non-null    object
 1   infants            435 non-null    int64 
 2   water              435 non-null    int64 
 3   budget             435 non-null    int64 
 4   physician          435 non-null    int64 
 5   salvador           435 non-null    int64 
 6   religious          435 non-null    int64 
 7   satellite          435 non-null    int64 
 8   aid                435 non-null    int64 
 9   missile            435 non-null    int64 
 10  immigration        435 non-null    int64 
 11  synfuels           435 non-null    int64 
 12  education          435 non-null    int64 
 13  superfund          435 non-null    int64 
 14  crime              435 non-null    int64 
 15  duty_free_exports  435 non-null    int64 
 16  eaa_rsa            435 non-null    int64 
dtypes: int64(16), object(1)
memory usage: 57.9+ KB

votes.describe()

	infants	water	budget	physician	salvador	religious	satellite	aid	missile	immigration	synfuels	education	superfund	crime	duty_free_exports	eaa_rsa
count	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000	435.000000
mean	0.429885	0.558621	0.606897	0.406897	0.521839	0.650575	0.581609	0.590805	0.526437	0.512644	0.344828	0.393103	0.537931	0.609195	0.400000	0.857471
std	0.495630	0.497123	0.489002	0.491821	0.500098	0.477337	0.493863	0.492252	0.499876	0.500416	0.475859	0.489002	0.499133	0.488493	0.490462	0.349994
min	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
25%	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	1.000000
50%	0.000000	1.000000	1.000000	0.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	0.000000	0.000000	1.000000	1.000000	0.000000	1.000000
75%	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000
max	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000

Observations

The DataFrame has a total of 435 rows and 17 columns.
Except for 'party', all of the columns are of type int64.
The first two rows of the DataFrame consist of votes made by Republicans and the next three rows consist of votes made by Democrats.
The target variable in this DataFrame is 'party'.

Votes Visual EDA

The Numerical EDA we did gave us some very important information, such as the names and data types of the columns, and the dimensions of the DataFrame. Following this with some visual EDA will give us an even better understanding of the data. all the features in this dataset are binary; that is, they are either 0 or 1. So a different type of plot would be more useful here, such as Seaborn’s countplot.

def plot_countplot(column):
    plt.figure()
    sns.countplot(x=column, hue='party', data=votes, palette='RdBu')
    plt.xticks([0,1], ['No', 'Yes'])
    plt.show()
    
plot_countplot("education")

It seems like Democrats voted resoundingly against this bill, compared to Republicans. This is the kind of information that our machine learning model will seek to learn when we try to predict party affiliation solely based on voting behavior. An expert in U.S politics may be able to predict this without machine learning, but probably not instantaneously - and certainly not if we are dealing with hundreds of samples!

plot_countplot('infants')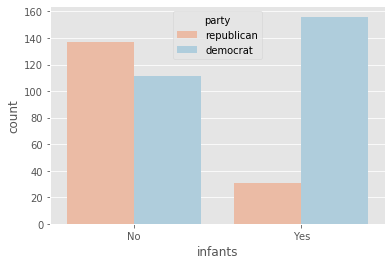

plot_countplot('water')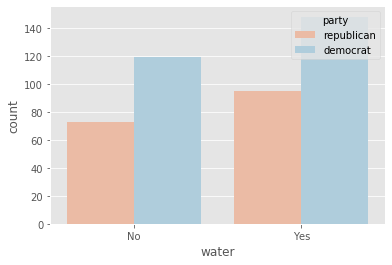

plot_countplot("budget")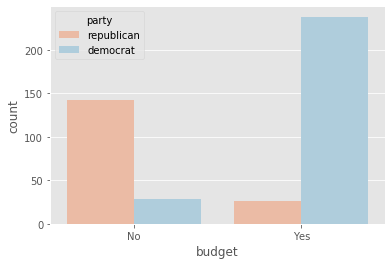

plot_countplot('physician')

plot_countplot('salvador')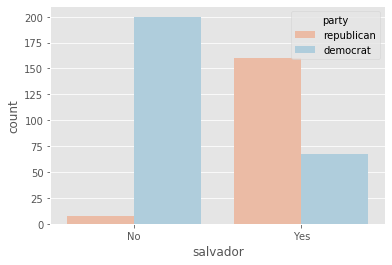

plot_countplot('religious')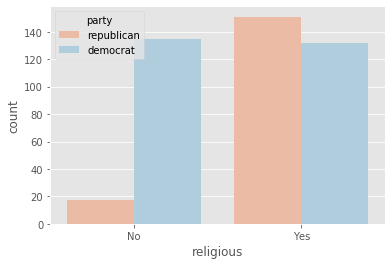

plot_countplot('satellite')

plot_countplot('aid')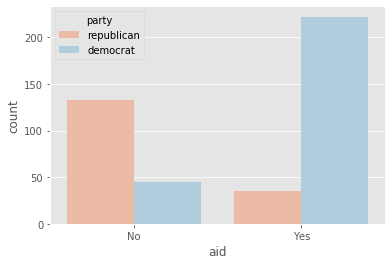

plot_countplot('missile')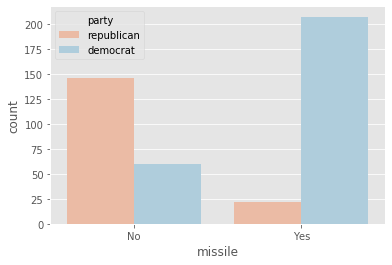

plot_countplot('immigration')

plot_countplot('synfuels')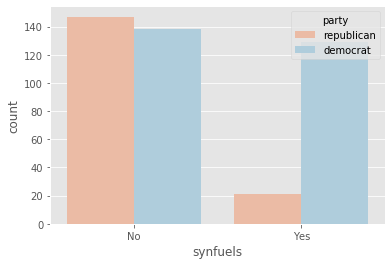

plot_countplot('superfund')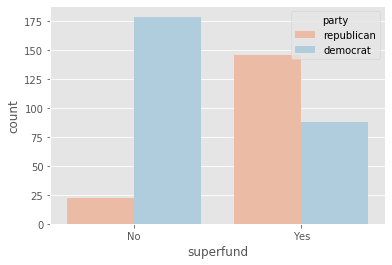

plot_countplot('crime')

plot_countplot('duty_free_exports')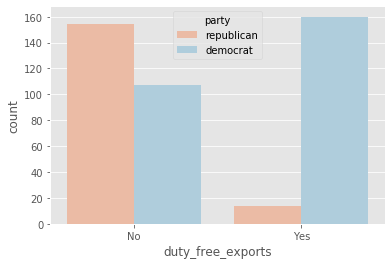

plot_countplot('eaa_rsa')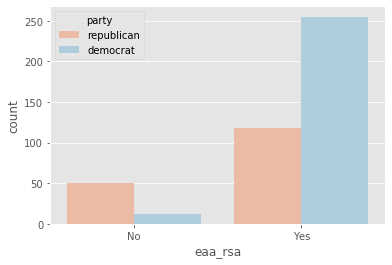

Observations

Democrats voted in favor of both 'satellite' and 'missile'

The classification challenge

k-Nearest Neighbors

Basic idea: Predict the label of a data point by

Looking at the ‘k’ closest labeled data points

Taking a majority vote

Scikit-learn fit and predict

All machine learning models implemented as Python classes

They implement the algorithms for learning and predicting

Store the information learned from the data

Training a model on the data = ‘fitting’ a model to the data

.fit() method

To predict the labels of new data: .predict() method

Iris k-NN: Intuition

_ = sns.scatterplot(data=df2, x="petal width (cm)", y="petal length (cm)", hue='target_names')
plt.show()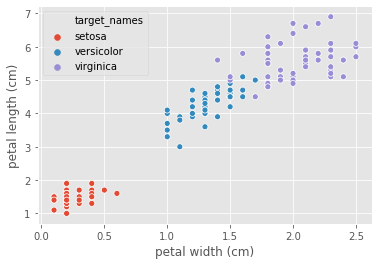

Iris dataset Using scikit-learn to fit a classier

knn = KNeighborsClassifier(n_neighbors=6)
knn.fit(iris['data'], iris['target'])

KNeighborsClassifier(n_neighbors=6)

iris['data'].shape

(150, 4)

iris['target'].shape

(150,)

Predicting on unlabeled data

X_new = np.array([[5.6, 2.8, 3.9, 1.1],
                 [5.7, 2.6, 3.8, 1.3],
                 [4.7, 3.2, 1.3, 0.2]])
prediction = knn.predict(X_new)
prediction

array([1, 1, 0])

k-Nearest Neighbors: Fit

Having explored the Congressional voting records dataset, it is time now to build our first classifier. We’ll will fit a k-Nearest Neighbors classifier to the voting dataset.

The features need to be in an array where each column is a feature and each row a different observation or data point - in this case, a Congressman’s voting record. The target needs to be a single column with the same number of observations as the feature data. We will name the feature array X and response variable y: This is in accordance with the common scikit-learn practice.

# Create arrays for the features and the response variable
y_votes = votes['party'].values
X_votes = votes.drop('party', axis=1).values

# Create a k-NN classifier with 6 neighbors
knn_votes = KNeighborsClassifier(n_neighbors=6)

# Fit the classifier to the data
knn_votes.fit(X_votes, y_votes)

KNeighborsClassifier(n_neighbors=6)

Now that the k-NN classifier with 6 neighbors has been fit to the data, it can be used to predict the labels of new data points.

k-Nearest Neighbors: Predict

X_new_votes = pd.read_csv("datasets/X_new_votes.csv")
X_new_votes.head()

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0.696469	0.286139	0.226851	0.551315	0.719469	0.423106	0.980764	0.68483	0.480932	0.392118	0.343178	0.72905	0.438572	0.059678	0.398044	0.737995

Having fit a k-NN classifier, we can now use it to predict the label of a new data point.

# Predict and print the label for the new data point X_new
new_prediction = knn_votes.predict(X_new_votes)
print("Prediction: {}".format(new_prediction))

Prediction: ['democrat']

Measuring model performance

In classication, accuracy is a commonly used metric

Accuracy = Fraction of correct predictions

Which data should be used to compute accuracy?

How well will the model perform on new data?

Could compute accuracy on data used to fit classifier

NOT indicative of ability to generalize

Split data into training and test set

Fit/train the classifier on the training set

Make predictions on test set

Compare predictions with the known labels

Model complexity

Larger k = smoother decision boundary = less complex model

Smaller k = more complex model = can lead to overfitting

X_train_iris, X_test_iris, y_train_iris, y_test_iris = train_test_split(X, y, test_size=.3, random_state=21, stratify=y)
knn_iris = KNeighborsClassifier(n_neighbors=8)
knn_iris.fit(X_train_iris, y_train_iris)
y_pred_iris = knn_iris.predict(X_test_iris)

print(f"Test set predictions \n{y_pred_iris}")

Test set predictions 
[2 1 2 2 1 0 1 0 0 1 0 2 0 2 2 0 0 0 1 0 2 2 2 0 1 1 1 0 0 1 2 2 0 0 1 2 2
 1 1 2 1 1 0 2 1]

knn_iris.score(X_test_iris, y_test_iris)

0.9555555555555556

The digits recognition dataset

We’ll be working with the MNIST digits recognition dataset, which has 10 classes, the digits 0 through 9! A reduced version of the MNIST dataset is one of scikit-learn’s included datasets.

Each sample in this scikit-learn dataset is an 8x8 image representing a handwritten digit. Each pixel is represented by an integer in the range 0 to 16, indicating varying levels of black. Helpfully for the MNIST dataset, scikit-learn provides an 'images' key in addition to the 'data' and 'target' keys that we have seen with the Iris data. Because it is a 2D array of the images corresponding to each sample, this 'images' key is useful for visualizing the images. On the other hand, the 'data' key contains the feature array - that is, the images as a flattened array of 64 pixels.

# Load the digits dataset: digits
digits = datasets.load_digits()

# Print the keys and DESCR of the dataset
print(digits.keys())
print(digits.DESCR)

dict_keys(['data', 'target', 'frame', 'feature_names', 'target_names', 'images', 'DESCR'])
.. _digits_dataset:

Optical recognition of handwritten digits dataset
--------------------------------------------------

**Data Set Characteristics:**

    :Number of Instances: 5620
    :Number of Attributes: 64
    :Attribute Information: 8x8 image of integer pixels in the range 0..16.
    :Missing Attribute Values: None
    :Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
    :Date: July; 1998

This is a copy of the test set of the UCI ML hand-written digits datasets
https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits

The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.

Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.

For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.

.. topic:: References

  - C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
    Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
    Graduate Studies in Science and Engineering, Bogazici University.
  - E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
  - Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
    Linear dimensionalityreduction using relevance weighted LDA. School of
    Electrical and Electronic Engineering Nanyang Technological University.
    2005.
  - Claudio Gentile. A New Approximate Maximal Margin Classification
    Algorithm. NIPS. 2000.

# Print the shape of the images and data keys
print(digits.images.shape)
digits.data.shape

(1797, 8, 8)

(1797, 64)

# Display digit 1010
plt.imshow(digits.images[1010], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()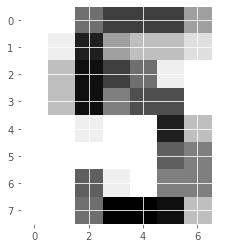

It looks like the image in question corresponds to the digit ‘5’. Now, can we build a classifier that can make this prediction not only for this image, but for all the other ones in the dataset?

Train/Test Split + Fit/Predict/Accuracy

Now that we have learned about the importance of splitting your data into training and test sets, it’s time to practice doing this on the digits dataset! After creating arrays for the features and target variable, we will split them into training and test sets, fit a k-NN classifier to the training data, and then compute its accuracy using the .score() method.

# Create feature and target arrays
X_digits = digits.data
y_digits = digits.target

# Split into training and test set
X_train_digits, X_test_digits, y_train_digits, y_test_digits = train_test_split(X_digits, y_digits, 
                                                                                test_size = 0.2, random_state= 42, 
                                                                                stratify=y_digits)

# Create a k-NN classifier with 7 neighbors: knn_digits
knn_digits = KNeighborsClassifier(n_neighbors=7)

# Fit the classifier to the training data
knn_digits.fit(X_train_digits, y_train_digits)

# Print the accuracy
knn_digits.score(X_test_digits, y_test_digits)

0.9833333333333333

Incredibly, this out of the box k-NN classifier with 7 neighbors has learned from the training data and predicted the labels of the images in the test set with 98% accuracy, and it did so in less than a second! This is one illustration of how incredibly useful machine learning techniques can be.

Overfitting and underfitting

We will now construct such a model complexity curve for the digits dataset! We will compute and plot the training and testing accuracy scores for a variety of different neighbor values.

By observing how the accuracy scores differ for the training and testing sets with different values of k, we will develop your intuition for overfitting and underfitting.

# Setup arrays to store train and test accuracies
neighbors_digits = np.arange(1, 9)
train_accuracy_digits = np.empty(len(neighbors_digits))
test_accuracy_digits = np.empty(len(neighbors_digits))

# Loop over different values of k
for i, k in enumerate(neighbors_digits):
    # Setup a k-NN Classifier with k neighbors: knn
    knn_digits = KNeighborsClassifier(n_neighbors=k)

    # Fit the classifier to the training data
    knn_digits.fit(X_train_digits, y_train_digits)
    
    #Compute accuracy on the training set
    train_accuracy_digits[i] = knn_digits.score(X_train_digits, y_train_digits)

    #Compute accuracy on the testing set
    test_accuracy_digits[i] = knn_digits.score(X_test_digits, y_test_digits)

# Generate plot
plt.title('k-NN: Varying Number of Neighbors')
plt.plot(neighbors_digits, test_accuracy_digits, label = 'Testing Accuracy')
plt.plot(neighbors_digits, train_accuracy_digits, label = 'Training Accuracy')
plt.legend()
plt.xlabel('Number of Neighbors')
plt.ylabel('Accuracy')
plt.show()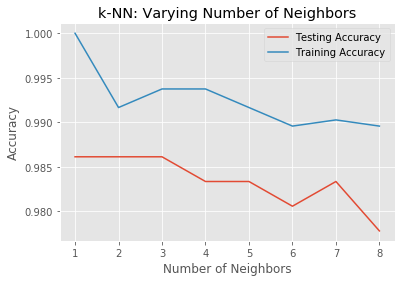

It looks like the test accuracy is highest when using 1 and35 neighbors. Using 8 neighbors or more seems to result in a simple model that underfits the data.

Regression

We used image and political datasets to predict binary and multiclass outcomes. But what if our problem requires a continuous outcome? Regression is best suited to solving such problems. We will explore the fundamental concepts in regression and apply them to predict the life expectancy in a given country using Gapminder data.

Introduction to regression

Example of an regression problem: A bike share company using time and weather data to predict the number of bikes being rented at any given hour. The target variable here - the number of bike rentals at any given hour - is quantitative, so this is best framed as a regression problem.

Boston housing data

boston = datasets.load_boston()
boston.data.shape

(506, 13)

boston.target.shape

(506,)

boston.feature_names

array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
       'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype='<U7')

boston_df = pd.DataFrame(boston.data, columns=boston.feature_names)
boston_df['MEDV'] = boston.target
boston_df.head()

	CRIM	ZN	INDUS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	396.90	5.33	36.2

Creating feature and target arrays for the boston dataset

X_boston = boston.data
y_boston = boston.target

Predicting house value from a single feature

X_boston_rooms = X_boston[:,5]
type(X_boston_rooms), type(y_boston)

(numpy.ndarray, numpy.ndarray)

y_boston = y_boston.reshape(-1,1)
X_boston_rooms = X_boston_rooms.reshape(-1,1)

Plotting house value vs. number of rooms

plt.scatter(X_boston_rooms, y_boston)
plt.ylabel('Value of house /1000 ($)')
plt.xlabel('Number of rooms')
plt.show();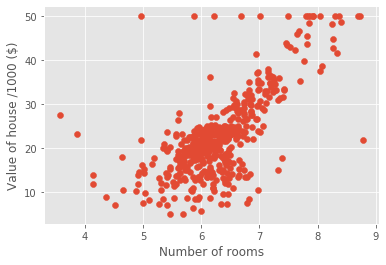

Fitting a regression model

reg_boston = LinearRegression()
reg_boston.fit(X_boston_rooms, y_boston)
boston_prediction_space = np.linspace(min(X_boston_rooms), max(X_boston_rooms)).reshape(-1,1)

plt.scatter(X_boston_rooms, y_boston, color="blue")
plt.plot(boston_prediction_space, reg_boston.predict(boston_prediction_space), color='black', linewidth=3)
plt.show()

Importing Gapminder data for supervised learning

We will work with Gapminder data that we have consolidated into one CSV file.

Specifically, our goal will be to use this data to predict the life expectancy in a given country based on features such as the country’s GDP, fertility rate, and population.

Since the target variable here is quantitative, this is a regression problem. To begin, we will fit a linear regression with just one feature: 'fertility', which is the average number of children a woman in a given country gives birth to.

Before that, however, we need to import the data and get it into the form needed by scikit-learn. This involves creating feature and target variable arrays. Furthermore, since we are going to use only one feature to begin with, we need to do some reshaping using NumPy’s .reshape() method.

# Read the CSV file into a DataFrame: gapminder_df
gapminder = pd.read_csv("datasets/gapminder.csv")

# Create arrays for features and target variable
y_gapminder = gapminder.life.values
X_gapminder = gapminder.fertility.values

# Print the dimensions of X and y before reshaping
print("Dimensions of y before reshaping: {}".format(y_gapminder.shape))
print("Dimensions of X before reshaping: {}".format(X_gapminder.shape))

# Reshape X and y
y_gapminder = y_gapminder.reshape(-1,1)
X_gapminder = X_gapminder.reshape(-1,1)

# Print the dimensions of X and y after reshaping
print("Dimensions of y after reshaping: {}".format(y_gapminder.shape))
print("Dimensions of X after reshaping: {}".format(X_gapminder.shape))

Dimensions of y before reshaping: (139,)
Dimensions of X before reshaping: (139,)
Dimensions of y after reshaping: (139, 1)
Dimensions of X after reshaping: (139, 1)

Exploring the Gapminder data

As always, it is important to explore the data before building models.

sns.heatmap(gapminder.corr(), square=True, cmap="RdYlGn")
plt.show()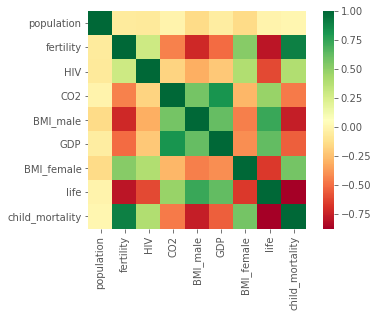

Cells that are in green show positive correlation, while cells that are in red show negative correlation. life and fertility are negatively correlated. GDP and life are positively correlated

gapminder.head()

	population	fertility	HIV	CO2	BMI_male	GDP	BMI_female	life	child_mortality
0	34811059.0	2.73	0.1	3.328945	24.59620	12314.0	129.9049	75.3	29.5
1	19842251.0	6.43	2.0	1.474353	22.25083	7103.0	130.1247	58.3	192.0
2	40381860.0	2.24	0.5	4.785170	27.50170	14646.0	118.8915	75.5	15.4
3	2975029.0	1.40	0.1	1.804106	25.35542	7383.0	132.8108	72.5	20.0
4	21370348.0	1.96	0.1	18.016313	27.56373	41312.0	117.3755	81.5	5.2

gapminder.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 139 entries, 0 to 138
Data columns (total 9 columns):
 #   Column           Non-Null Count  Dtype  
---  ------           --------------  -----  
 0   population       139 non-null    float64
 1   fertility        139 non-null    float64
 2   HIV              139 non-null    float64
 3   CO2              139 non-null    float64
 4   BMI_male         139 non-null    float64
 5   GDP              139 non-null    float64
 6   BMI_female       139 non-null    float64
 7   life             139 non-null    float64
 8   child_mortality  139 non-null    float64
dtypes: float64(9)
memory usage: 9.9 KB

The DataFrame has 139 samples (or rows) and 9 columns.

gapminder.describe()

	population	fertility	HIV	CO2	BMI_male	GDP	BMI_female	life	child_mortality
count	1.390000e+02	139.000000	139.000000	139.000000	139.000000	139.000000	139.000000	139.000000	139.000000
mean	3.549977e+07	3.005108	1.915612	4.459874	24.623054	16638.784173	126.701914	69.602878	45.097122
std	1.095121e+08	1.615354	4.408974	6.268349	2.209368	19207.299083	4.471997	9.122189	45.724667
min	2.773150e+05	1.280000	0.060000	0.008618	20.397420	588.000000	117.375500	45.200000	2.700000
25%	3.752776e+06	1.810000	0.100000	0.496190	22.448135	2899.000000	123.232200	62.200000	8.100000
50%	9.705130e+06	2.410000	0.400000	2.223796	25.156990	9938.000000	126.519600	72.000000	24.000000
75%	2.791973e+07	4.095000	1.300000	6.589156	26.497575	23278.500000	130.275900	76.850000	74.200000
max	1.197070e+09	7.590000	25.900000	48.702062	28.456980	126076.000000	135.492000	82.600000	192.000000

The mean of life is 69.602878

The basics of linear regression

Regression mechanics

\(y = ax + b\)

\(y\) = target

\(x\) = single feature

\(a\), \(b\) = parameters of model

How do we choose \(a\) and \(b\)?

Define an error functions for any given lineChoose the line that minimizes the error function

Ordinary least squares(OLS): Minimize sum of squares of residuals

Linear regression in higher dimensions

\(y=a_1x_1+a_2x_2+b\)

To fit a linear regression model here:

Need to specify 3 variables

In higher dimensions:

Must specify coefcient for each feature and the variable \(b\)

\(y=a_1x_1+a_2x_2+a_3x_3+...+a_nx_n+b\)

Scikit-learn API works exactly the same way:

Pass two arrays: Features, and target

Linear regression on all features in boston dataset

X_train_boston, X_test_boston, y_train_boston, y_test_boston = train_test_split(X_boston, y_boston, 
                                                                                test_size=.3, random_state=42)
reg_all_boston = LinearRegression()
reg_all_boston.fit(X_train_boston, y_train_boston)
y_pred_boston = reg_all_boston.predict(X_test_boston)
reg_all_boston.score(X_test_boston, y_test_boston)

0.7112260057484925

Fit & predict for regression in gapminder dataset

We will fit a linear regression and predict life expectancy using just one feature. We will use the 'fertility' feature of the Gapminder dataset. Since the goal is to predict life expectancy, the target variable here is 'life'.

sns.scatterplot(data=gapminder, x="fertility", y="life")
plt.show()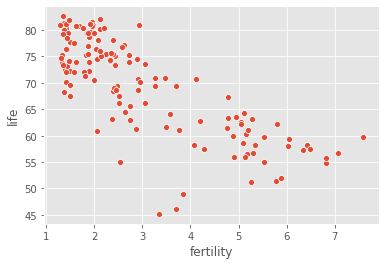

As you can see, there is a strongly negative correlation, so a linear regression should be able to capture this trend. Our job is to fit a linear regression and then predict the life expectancy, overlaying these predicted values on the plot to generate a regression line. We will also compute and print the \(R^2\) score using sckit-learn’s .score() method.

# Create the regressor: reg
reg_gapminder = LinearRegression()

# Create the prediction space
prediction_space = np.linspace(min(X_gapminder), max(X_gapminder)).reshape(-1,1)

# Fit the model to the data
reg_gapminder.fit(X_gapminder,y_gapminder)

# Compute predictions over the prediction space: y_pred
y_pred_gapminder = reg_gapminder.predict(prediction_space)

# Print R^2 
print(reg_gapminder.score(X_gapminder, y_gapminder))

0.6192442167740035

# Plot regression line
sns.scatterplot(data=gapminder, x="fertility", y="life")
plt.plot(prediction_space, y_pred_gapminder, color='black', linewidth=3)
plt.show()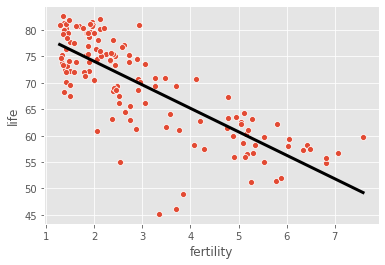

Notice how the line captures the underlying trend in the data. And the performance is quite decent for this basic regression model with only one feature!

Train/test split for regression

train and test sets are vital to ensure that the supervised learning model is able to generalize well to new data. This was true for classification models, and is equally true for linear regression models.

We will split the Gapminder dataset into training and testing sets, and then fit and predict a linear regression over all features. In addition to computing the \(R^2\) score, we will also compute the Root Mean Squared Error (RMSE), which is another commonly used metric to evaluate regression models.

X_gapminder = gapminder.drop("life", axis=1).values

# Create training and test sets
X_train_gapminder, X_test_gapminder, y_train_gapminder, y_test_gapminder = train_test_split(X_gapminder, y_gapminder, test_size = .3, random_state=42)

# Create the regressor: reg_all
reg_all_gapminder = LinearRegression()

# Fit the regressor to the training data
reg_all_gapminder.fit(X_train_gapminder, y_train_gapminder)

# Predict on the test data: y_pred
y_pred_gapminder = reg_all_gapminder.predict(X_test_gapminder)

# Compute and print R^2 and RMSE
print("R^2: {}".format(reg_all_gapminder.score(X_test_gapminder, y_test_gapminder)))
rmse_gapminder = np.sqrt(mean_squared_error(y_test_gapminder, y_pred_gapminder))
print("Root Mean Squared Error: {}".format(rmse_gapminder))

R^2: 0.8380468731430059
Root Mean Squared Error: 3.247601080037022

Using all features has improved the model score. This makes sense, as the model has more information to learn from. However, there is one potential pitfall to this process. Can you spot it?

Cross-validation

Cross-validation motivation

Model performance is dependent on way the data is split

Not representative of the model’s ability to generalize

Solution: Cross-validation!

Cross-validation and model performance

5 folds = 5-fold CV

10 folds = 10-fold CV

k folds = k-fold CV

More folds = More computationally expensive

Cross-validation in scikit-learn: Boston

cv_results_boston = cross_val_score(reg_all_boston, X_boston, y_boston, cv=5)
cv_results_boston

array([ 0.63919994,  0.71386698,  0.58702344,  0.07923081, -0.25294154])

np.mean(cv_results_boston)

0.353275924395884

np.median(cv_results_boston)

0.5870234363057776

5-fold cross-validation

Cross-validation is a vital step in evaluating a model. It maximizes the amount of data that is used to train the model, as during the course of training, the model is not only trained, but also tested on all of the available data.

We will practice 5-fold cross validation on the Gapminder data. By default, scikit-learn’s cross_val_score() function uses R2 as the metric of choice for regression. Since We are performing 5-fold cross-validation, the function will return 5 scores. We will compute these 5 scores and then take their average.

# Compute 5-fold cross-validation scores: cv_scores
cv_scores_gapminder = cross_val_score(reg_gapminder, X_gapminder, y_gapminder, cv=5)

# Print the 5-fold cross-validation scores
print(cv_scores_gapminder)

print("Average 5-Fold CV Score: {}".format(np.mean(cv_scores_gapminder)))

[0.81720569 0.82917058 0.90214134 0.80633989 0.94495637]
Average 5-Fold CV Score: 0.8599627722793267

Now that we have cross-validated your model, we can more confidently evaluate its predictions.

K-Fold CV comparison

Warning

Cross validation is essential but do not forget that the more folds you use, the more computationally expensive cross-validation becomes.

%timeit cross_val_score(reg_gapminder, X_gapminder, y_gapminder, cv=3)

8.03 ms ± 1.01 ms per loop (mean ± std. dev. of 7 runs, 100 loops each)

%timeit cross_val_score(reg_gapminder, X_gapminder, y_gapminder, cv=10)

31.8 ms ± 1.21 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

# Perform 3-fold CV
cvscores_3_gapminder = cross_val_score(reg_gapminder, X_gapminder, y_gapminder, cv=3)
print(np.mean(cvscores_3_gapminder))

# Perform 10-fold CV
cvscores_10_gapminder = cross_val_score(reg_gapminder, X_gapminder, y_gapminder, cv=10)
print(np.mean(cvscores_10_gapminder))

0.8718712782621969
0.8436128620131095

Regularized regression

Why regularize?

Recall: Linear regression minimizes a loss function

It chooses a coefcient for each feature variable

Large coefcients can lead to overtting

Penalizing large coefcients: Regularization

Ridge regression

Loss function = OLS loss function + \(\alpha * \sum_{i=1}^{n} a_i^2\)

Alpha: Parameter we need to choose

Picking alpha here is similar to picking k in k-NN

Hyperparameter tuning

Alpha controls model complexity

Alpha = 0: We get back OLS (Can lead to overtting)

Very high alpha: Can lead to undertting

Lasso regression

Loss function = OLS loss function + \(\alpha * \sum_{i=1}^{n} |a_i|\)

Lasso regression for feature selection

Can be used to select important features of a dataset

Shrinks the coefcients of less important features to exactly 0

Ridge regression in scikit-learn: Boston

ridge_boston = Ridge(alpha=.1, normalize=True)
ridge_boston.fit(X_train_boston, y_train_boston)
ridge_pred_boston = ridge_boston.predict(X_test_boston)
ridge_boston.score(X_test_boston, y_test_boston)

0.6996938275127311

Lasso regression in scikit-learn: Boston

lasso_boston = Lasso(alpha=.1, normalize=True)
lasso_boston.fit(X_train_boston, y_train_boston)
lasso_pred_boston = lasso_boston.predict(X_test_boston)
lasso_boston.score(X_test_boston, y_test_boston)

0.5950229535328551

Lasso for feature selection in scikit-learn: Boston

names_boston = boston.feature_names
lasso_boston_2 = Lasso(alpha=.1)
lasso_coef_boston = lasso_boston_2.fit(X_boston, y_boston).coef_
_ = plt.plot(range(len(names_boston)), lasso_coef_boston)
_ = plt.xticks(range(len(names_boston)), names_boston, rotation=60)
_ = plt.ylabel("Coefficients")
plt.show()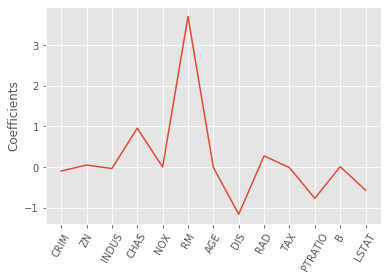

Regularization I: Lasso

We saw how Lasso selected out the ‘RM’ feature as being the most important for predicting Boston house prices, while shrinking the coefficients of certain other features to 0. Its ability to perform feature selection in this way becomes even more useful when you are dealing with data involving thousands of features.

We will fit a lasso regression to the Gapminder data we have been working with and plot the coefficients. Just as with the Boston data.

df_columns_gapminder = pd.Index(['population', 'fertility', 'HIV', 'CO2', 'BMI_male', 'GDP',
       'BMI_female', 'child_mortality'],
      dtype='object')

# Instantiate a lasso regressor: lasso
lasso_gapminder = Lasso(alpha=.4, normalize=True)

# Fit the regressor to the data
lasso_gapminder.fit(X_gapminder,y_gapminder)

# Compute and print the coefficients
lasso_coef_gapminder = lasso_gapminder.fit(X_gapminder,y_gapminder).coef_
print(lasso_coef_gapminder)

# Plot the coefficients
plt.plot(range(len(df_columns_gapminder)), lasso_coef_gapminder)
plt.xticks(range(len(df_columns_gapminder)), df_columns_gapminder.values, rotation=60)
plt.margins(0.02)
plt.show()

[-0.         -0.         -0.          0.          0.          0.
 -0.         -0.07087587]

According to the lasso algorithm, it seems like 'child_mortality' is the most important feature when predicting life expectancy.

Regularization II: Ridge

Lasso is great for feature selection, but when building regression models, Ridge regression should be the first choice.

lasso performs regularization by adding to the loss function a penalty term of the absolute value of each coefficient multiplied by some alpha. This is also known as \(L1\) regularization because the regularization term is the \(L1\) norm of the coefficients. This is not the only way to regularize, however.

def display_plot(cv_scores, cv_scores_std):
    """plots the R^2 score as well as standard error for each alpha"""
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    ax.plot(alpha_space_gapminder, cv_scores)

    std_error = cv_scores_std / np.sqrt(10)

    ax.fill_between(alpha_space_gapminder, cv_scores + std_error, cv_scores - std_error, alpha=0.2)
    ax.set_ylabel('CV Score +/- Std Error')
    ax.set_xlabel('Alpha')
    ax.axhline(np.max(cv_scores), linestyle='--', color='.5')
    ax.set_xlim([alpha_space_gapminder[0], alpha_space_gapminder[-1]])
    ax.set_xscale('log')
    plt.show()

If instead we took the sum of the squared values of the coefficients multiplied by some alpha - like in Ridge regression - we would be computing the \(L2\) norm. We will fit ridge regression models over a range of different alphas, and plot cross-validated \(R^2\) scores for each, using this function display_plot, which plots the \(R^2\) score as well as standard error for each alpha:

# Setup the array of alphas and lists to store scores
alpha_space_gapminder = np.logspace(-4, 0, 50)
ridge_scores_gapminder = []
ridge_scores_std_gapminder = []

# Create a ridge regressor: ridge
ridge_gapminder = Ridge(normalize=True)

# Compute scores over range of alphas
for alpha in alpha_space_gapminder:

    # Specify the alpha value to use: ridge.alpha
    ridge_gapminder.alpha = alpha
    
    # Perform 10-fold CV: ridge_cv_scores
    ridge_cv_scores_gapminder = cross_val_score(ridge_gapminder, X_gapminder, y_gapminder, cv=10)
    
    # Append the mean of ridge_cv_scores to ridge_scores
    ridge_scores_gapminder.append(np.mean(ridge_cv_scores_gapminder))
    
    # Append the std of ridge_cv_scores to ridge_scores_std
    ridge_scores_std_gapminder.append(np.std(ridge_cv_scores_gapminder))

# Display the plot
display_plot(ridge_scores_gapminder, ridge_scores_std_gapminder)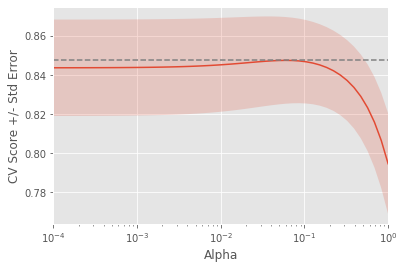

the cross-validation scores change with different alphas.

Fine-tuning model

Having trained a model, the next task is to evaluate its performance. We will explore some of the other metrics available in scikit-learn that will allow us to assess the model’s performance in a more nuanced manner.

How good is your model?

Classication metrics

Measuring model performance with accuracy:

Fraction of correctly classied samples

Not always a useful metric

Class imbalance example: Emails

Spam classication

99% of emails are real; 1% of emails are spam

Could build a classier that predicts ALL emails as real

99% accurate!

But horrible at actually classifying spam

Fails at its original purpose

Need more nuanced metrics

Diagnosing classication predictions

Confusion matrix

Accuracy: \(\frac{tp+tn}{tp+tn+fp+fn}\)

Metrics from the confusion matrix

Precision: \(\frac{tp}{tp+fp}\)

Recal \(\frac{tp}{tp+fn}\)

F1score: \(2.\frac{precision.recal}{precision+recall}\)

High precision: Not many real emails predicted as spam

High recall: Predicted most spam emails correctly

Confusion matrix in scikit-learn: iris dataset

confusion_matrix(y_test_iris, y_pred_iris)

array([[15,  0,  0],
       [ 0, 14,  1],
       [ 0,  1, 14]], dtype=int64)

print(classification_report(y_test_iris, y_pred_iris))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        15
           1       0.93      0.93      0.93        15
           2       0.93      0.93      0.93        15

    accuracy                           0.96        45
   macro avg       0.96      0.96      0.96        45
weighted avg       0.96      0.96      0.96        45

X_train_votes, X_test_votes, y_train_votes, y_test_votes = train_test_split(X_votes, y_votes, test_size=.4, random_state=42)
knn_votes = KNeighborsClassifier(n_neighbors=8)
knn_votes.fit(X_train_votes, y_train_votes)
y_pred_votes = knn_votes.predict(X_test_votes)

confusion_matrix(y_test_votes, y_pred_votes)

array([[108,   7],
       [  4,  55]], dtype=int64)

print(classification_report(y_test_votes, y_pred_votes))

              precision    recall  f1-score   support

    democrat       0.96      0.94      0.95       115
  republican       0.89      0.93      0.91        59

    accuracy                           0.94       174
   macro avg       0.93      0.94      0.93       174
weighted avg       0.94      0.94      0.94       174

The support gives the number of samples of the true response that lie in that class, the support was the number of Republicans or Democrats in the test set on which the classification report was computed. The precision, recall, and f1-score columns, then, gave the respective metrics for that particular class.

Metrics for classification

We evaluated the performance of k-NN classifier based on its accuracy. However, accuracy is not always an informative metric. We will dive more deeply into evaluating the performance of binary classifiers by computing a confusion matrix and generating a classification report.

We’ll work with the PIMA Indians dataset obtained from the UCI Machine Learning Repository. The goal is to predict whether or not a given female patient will contract diabetes based on features such as BMI, age, and number of pregnancies. Therefore, it is a binary classification problem. A target value of 0 indicates that the patient does not have diabetes, while a value of 1 indicates that the patient does have diabetes.

pidd = pd.read_csv("datasets/pima_indians_diabetes_database.csv")
pidd.head()

	pregnancies	glucose	diastolic	triceps	insulin	bmi	dpf	age	diabetes
0	6	148	72	35.00000	155.548223	33.6	0.627	50	1
1	1	85	66	29.00000	155.548223	26.6	0.351	31	0
2	8	183	64	29.15342	155.548223	23.3	0.672	32	1
3	1	89	66	23.00000	94.000000	28.1	0.167	21	0
4	0	137	40	35.00000	168.000000	43.1	2.288	33	1

We will train a k-NN classifier to the data and evaluate its performance by generating a confusion matrix and classification report.

y_pidd = pidd.diabetes.values
X_pidd = pidd.drop("diabetes", axis=1).values

# Create training and test set
X_train_pidd, X_test_pidd, y_train_pidd, y_test_pidd = train_test_split(X_pidd, y_pidd, test_size=.4, random_state=42)

# Instantiate a k-NN classifier: knn
knn_pidd = KNeighborsClassifier(n_neighbors=6)

# Fit the classifier to the training data
knn_pidd.fit(X_train_pidd, y_train_pidd)

# Predict the labels of the test data: y_pred
y_pred_pidd = knn_pidd.predict(X_test_pidd)

# Generate the confusion matrix and classification report
print(confusion_matrix(y_test_pidd, y_pred_pidd))
print(classification_report(y_test_pidd, y_pred_pidd))

[[176  30]
 [ 52  50]]
              precision    recall  f1-score   support

           0       0.77      0.85      0.81       206
           1       0.62      0.49      0.55       102

    accuracy                           0.73       308
   macro avg       0.70      0.67      0.68       308
weighted avg       0.72      0.73      0.72       308

By analyzing the confusion matrix and classification report, we can get a much better understanding of your classifier’s performance.

Logistic regression and the ROC curve

Logistic regression for binary classication

Logistic regression outputs probabilities

If the probability ‘p’ is greater than 0.5:

The data is labeled ‘1’

If the probability ‘p’ is less than 0.5:

The data is labeled ‘0’

Probability thresholds

By default, logistic regression threshold = 0.5

Not specific to logistic regression

k-NN classifiers also have thresholds

What happens if we vary the threshold?

Building a logistic regression model

Time to build our first logistic regression model! scikit-learn makes it very easy to try different models, since the Train-Test-Split/Instantiate/Fit/Predict paradigm applies to all classifiers and regressors - which are known in scikit-learn as ‘estimators’.

# Create the classifier: logreg
logreg_pidd = LogisticRegression()

# Fit the classifier to the training data
logreg_pidd.fit(X_train_pidd, y_train_pidd)

# Predict the labels of the test set: y_pred
y_pred_logreg_pidd = logreg_pidd.predict(X_test_pidd)

# Compute and print the confusion matrix and classification report
print(confusion_matrix(y_test_pidd, y_pred_logreg_pidd))
print(classification_report(y_test_pidd, y_pred_logreg_pidd))

[[171  35]
 [ 35  67]]
              precision    recall  f1-score   support

           0       0.83      0.83      0.83       206
           1       0.66      0.66      0.66       102

    accuracy                           0.77       308
   macro avg       0.74      0.74      0.74       308
weighted avg       0.77      0.77      0.77       308

Precision-recall Curve

the precision-recall curve is generated by plotting the precision and recall for different thresholds.

\[ precision = \frac{TP}{TP+FP} \] \[ recall = \frac{TP}{TP+FN} \]

disp = plot_precision_recall_curve(logreg_pidd, X_test_pidd, y_test_pidd)
disp.ax_.set_title('Precision-Recall curve: ')

Text(0.5, 1.0, 'Precision-Recall curve: ')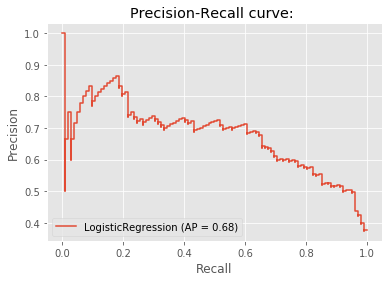

A recall of 1 corresponds to a classifier with a low threshold in which all females who contract diabetes were correctly classified as such, at the expense of many misclassifications of those who did not have diabetes.
Precision is undefined for a classifier which makes no positive predictions, that is, classifies everyone as not having diabetes.
When the threshold is very close to 1, precision is also 1, because the classifier is absolutely certain about its predictions.

Plotting an ROC curve

Classification reports and confusion matrices are great methods to quantitatively evaluate model performance, while ROC curves provide a way to visually evaluate models. most classifiers in scikit-learn have a .predict_proba() method which returns the probability of a given sample being in a particular class. Having built a logistic regression model, we’ll now evaluate its performance by plotting an ROC curve. In doing so, we’ll make use of the .predict_proba() method and become familiar with its functionality.

# Compute predicted probabilities: y_pred_prob
y_pred_prob_pidd = logreg_pidd.predict_proba(X_test_pidd)[:,1]

# Generate ROC curve values: fpr, tpr, thresholds
fpr_pidd, tpr_pidd, thresholds_pidd = roc_curve(y_test_pidd, y_pred_prob_pidd)

# Plot ROC curve
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr_pidd, tpr_pidd)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.show()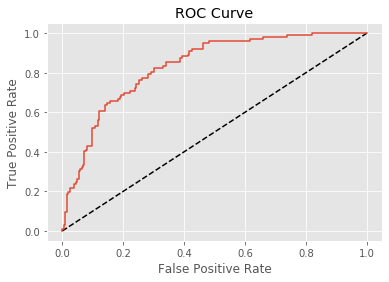

Area under the ROC curve

Area under the ROC curve (AUC)

Larger area under the ROC curve = better model

AUC computation

Say you have a binary classifier that in fact is just randomly making guesses. It would be correct approximately 50% of the time, and the resulting ROC curve would be a diagonal line in which the True Positive Rate and False Positive Rate are always equal. The Area under this ROC curve would be 0.5. This is one way in which the AUC is an informative metric to evaluate a model. If the AUC is greater than 0.5, the model is better than random guessing. Always a good sign!

We’ll calculate AUC scores using the roc_auc_score() function from sklearn.metrics as well as by performing cross-validation on the diabetes dataset.

# Compute and print AUC score
print("AUC: {}".format(roc_auc_score(y_test_pidd, y_pred_prob_pidd)))

# Compute cross-validated AUC scores: cv_auc
cv_auc_pidd = cross_val_score(logreg_pidd, X_pidd, y_pidd, cv=5, scoring="roc_auc")

# Print list of AUC scores
print("AUC scores computed using 5-fold cross-validation: {}".format(cv_auc_pidd))

AUC: 0.8329050066628594
AUC scores computed using 5-fold cross-validation: [0.81962963 0.80537037 0.82555556 0.87377358 0.82509434]

Hyperparameter tuning

Hyperparameter tuning

Linear regression: Choosing parameters

Ridge/lasso regression: Choosing alpha

k-Nearest Neighbors: Choosing n_neighbors

Parameters like alpha and k: Hyperparameters

Hyperparameters cannot be learned by tting the model

Choosing the correct hyperparameter

Try a bunch of different hyperparameter values

Fit all of them separately

See how well each performs

Choose the best performing one

It is essential to use cross-validation

GridSearchCV in scikit-learn votes dataset

param_grid_votes = {"n_neighbors":np.arange(1,50)}
knn_votes = KNeighborsClassifier()
knn_cv_votes = GridSearchCV(knn_votes, param_grid=param_grid_votes, cv=5)
knn_cv_votes.fit(X_votes, y_votes)
knn_cv_votes.best_params_

{'n_neighbors': 4}

knn_cv_votes.best_score_

0.9333333333333333

Hyperparameter tuning with GridSearchCV

logistic regression also has a regularization parameter: \(C\). \(C\) controls the inverse of the regularization strength, and this is what we will tune. A large \(C\) can lead to an overfit model, while a small \(C\) can lead to an underfit model.

# Setup the hyperparameter grid
c_space_pidd = np.logspace(-5, 8, 15)
param_grid_pidd = {'C': c_space_pidd}

# Instantiate the GridSearchCV object: logreg_cv
logreg_cv_pidd = GridSearchCV(logreg_pidd, param_grid_pidd, cv=5)

# Fit it to the data
logreg_cv_pidd.fit(X_pidd,y_pidd)

# Print the tuned parameters and score
print("Tuned Logistic Regression Parameters: {}".format(logreg_cv_pidd.best_params_)) 
print("Best score is {}".format(logreg_cv_pidd.best_score_))

Tuned Logistic Regression Parameters: {'C': 1389495.494373136}
Best score is 0.7787029963500551

Hyperparameter tuning with RandomizedSearchCV

GridSearchCV can be computationally expensive, especially if you are searching over a large hyperparameter space and dealing with multiple hyperparameters. A solution to this is to use RandomizedSearchCV, in which not all hyperparameter values are tried out. Instead, a fixed number of hyperparameter settings is sampled from specified probability distributions.

Decision trees have many parameters that can be tuned, such as max_features, max_depth, and min_samples_leaf: This makes it an ideal use case for RandomizedSearchCV. Our goal is to use RandomizedSearchCV to find the optimal hyperparameters.

# Setup the parameters and distributions to sample from: param_dist
param_dist_pidd = {"max_depth": [3, None],
              "max_features": randint(1, 9),
              "min_samples_leaf": randint(1, 9),
              "criterion": ["gini", "entropy"]}

# Instantiate a Decision Tree classifier: tree
tree_pidd = DecisionTreeClassifier()

# Instantiate the RandomizedSearchCV object: tree_cv
tree_cv_pidd = RandomizedSearchCV(tree_pidd, param_dist_pidd, cv=5)

# Fit it to the data
tree_cv_pidd.fit(X,y)

# Print the tuned parameters and score
print("Tuned Decision Tree Parameters: {}".format(tree_cv_pidd.best_params_))
print("Best score is {}".format(tree_cv_pidd.best_score_))

Tuned Decision Tree Parameters: {'criterion': 'gini', 'max_depth': 3, 'max_features': 3, 'min_samples_leaf': 2}
Best score is 0.96

Note

RandomizedSearchCV will never outperform GridSearchCV. Instead, it is valuable because it saves on computation time.

Hold-out set for final evaluation

Hold-out set reasoning

How well can the model perform on never before seen data?

Using ALL data for cross-validation is not ideal

Split data into training and hold-out set at the beginning

Perform grid search cross-validation on training set

Choose best hyperparameters and evaluate on hold-out set

Hold-out set in practice I: Classification

You will now practice evaluating a model with tuned hyperparameters on a hold-out set. In addition to \(C\), logistic regression has a 'penalty' hyperparameter which specifies whether to use 'l1' or 'l2' regularization. Our job is to create a hold-out set, tune the 'C' and 'penalty' hyperparameters of a logistic regression classifier using GridSearchCV on the training set.

param_grid_pidd['penalty'] = ['l1', 'l2']

# Instantiate the GridSearchCV object: logreg_cv
logreg_cv_pidd = GridSearchCV(logreg_pidd, param_grid_pidd, cv=5)

# Fit it to the training data
logreg_cv_pidd.fit(X_train_pidd, y_train_pidd)

# Print the optimal parameters and best score
print("Tuned Logistic Regression Parameter: {}".format(logreg_cv_pidd.best_params_))
print("Tuned Logistic Regression Accuracy: {}".format(logreg_cv_pidd.best_score_))

Tuned Logistic Regression Parameter: {'C': 100000000.0, 'penalty': 'l2'}
Tuned Logistic Regression Accuracy: 0.7717391304347827

Hold-out set in practice II: Regression

Lasso used the \(L1\) penalty to regularize, while ridge used the \(L2\) penalty. There is another type of regularized regression known as the elastic net. In elastic net regularization, the penalty term is a linear combination of the \(L1\) and \(L2\) penalties:

\[ a∗L1+b∗L2 \]

In scikit-learn, this term is represented by the 'l1_ratio' parameter: An 'l1_ratio' of 1 corresponds to an \(L1\) penalty, and anything lower is a combination of \(L1\) and \(L2\).

We will GridSearchCV to tune the 'l1_ratio' of an elastic net model trained on the Gapminder data.

# Create the hyperparameter grid
l1_space_gapminder = np.linspace(0, 1, 30)
param_grid_gapminder = {'l1_ratio': l1_space_gapminder}

# Instantiate the ElasticNet regressor: elastic_net
elastic_net_gapminder = ElasticNet()

# Setup the GridSearchCV object: gm_cv
gm_cv_gapminder = GridSearchCV(elastic_net_gapminder, param_grid_gapminder, cv=5)

# Fit it to the training data
gm_cv_gapminder.fit(X_train_gapminder, y_train_gapminder)

# Predict on the test set and compute metrics
y_pred_gapminder = gm_cv_gapminder.predict(X_test_gapminder)
r2_gapminder = gm_cv_gapminder.score(X_test_gapminder, y_test_gapminder)
mse_gapminder = mean_squared_error(y_test_gapminder, y_pred_gapminder)
print("Tuned ElasticNet l1 ratio: {}".format(gm_cv_gapminder.best_params_))
print("Tuned ElasticNet R squared: {}".format(r2_gapminder))
print("Tuned ElasticNet MSE: {}".format(mse_gapminder))

Tuned ElasticNet l1 ratio: {'l1_ratio': 0.0}
Tuned ElasticNet R squared: 0.8442220994403307
Tuned ElasticNet MSE: 10.144762014599413

Preprocessing and pipelines

Pipelines, and how scikit-learn allows for transformers and estimators to be chained together and used as a single unit. Preprocessing techniques will be introduced as a way to enhance model performance, and pipelines will tie together concepts from previous sections.

Preprocessing data

Dealing with categorical features

Scikit-learn will not accept categorical features by default

Need to encode categorical features numerically

Convert to ‘dummy variables’

0: Observation was NOT that category

1: Observation was that category

Dealing with categorical features in Python

scikit-learn:

OneHotEncoder()

pandas:

get_dummies()

Automobile dataset

mpg:Target Variable
Origin:Categorical Feature

autos = pd.read_csv("datasets/autos.csv")
autos.head()

	mpg	displ	hp	weight	accel	origin	size
0	18.0	250.0	88	3139	14.5	US	15.0
1	9.0	304.0	193	4732	18.5	US	20.0
2	36.1	91.0	60	1800	16.4	Asia	10.0
3	18.5	250.0	98	3525	19.0	US	15.0
4	34.3	97.0	78	2188	15.8	Europe	10.0

autos.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 392 entries, 0 to 391
Data columns (total 7 columns):
 #   Column  Non-Null Count  Dtype  
---  ------  --------------  -----  
 0   mpg     392 non-null    float64
 1   displ   392 non-null    float64
 2   hp      392 non-null    int64  
 3   weight  392 non-null    int64  
 4   accel   392 non-null    float64
 5   origin  392 non-null    object 
 6   size    392 non-null    float64
dtypes: float64(4), int64(2), object(1)
memory usage: 21.6+ KB

autos.describe()

	mpg	displ	hp	weight	accel	size
count	392.000000	392.000000	392.000000	392.000000	392.000000	392.000000
mean	23.445918	194.411990	104.469388	2977.584184	15.541327	13.679847
std	7.805007	104.644004	38.491160	849.402560	2.758864	4.264458
min	9.000000	68.000000	46.000000	1613.000000	8.000000	7.500000
25%	17.000000	105.000000	75.000000	2225.250000	13.775000	10.000000
50%	22.750000	151.000000	93.500000	2803.500000	15.500000	10.000000
75%	29.000000	275.750000	126.000000	3614.750000	17.025000	20.000000
max	46.600000	455.000000	230.000000	5140.000000	24.800000	20.000000

autos.shape

(392, 7)

EDA w/ categorical feature

_ = sns.boxplot(data=autos, x="origin", y="mpg", order=['Asia', 'US', 'Europe'])
plt.show()

Encoding dummy variables

autos_origin = pd.get_dummies(autos)
autos_origin.head()

	mpg	displ	hp	weight	accel	size	origin_Asia	origin_Europe	origin_US
0	18.0	250.0	88	3139	14.5	15.0	0	0	1
1	9.0	304.0	193	4732	18.5	20.0	0	0	1
2	36.1	91.0	60	1800	16.4	10.0	1	0	0
3	18.5	250.0	98	3525	19.0	15.0	0	0	1
4	34.3	97.0	78	2188	15.8	10.0	0	1	0

autos_origin = autos_origin.drop("origin_Asia", axis=1)
autos_origin.head()

	mpg	displ	hp	weight	accel	size	origin_Europe	origin_US
0	18.0	250.0	88	3139	14.5	15.0	0	1
1	9.0	304.0	193	4732	18.5	20.0	0	1
2	36.1	91.0	60	1800	16.4	10.0	0	0
3	18.5	250.0	98	3525	19.0	15.0	0	1
4	34.3	97.0	78	2188	15.8	10.0	1	0

Linear regression with dummy variables

X_autos_origin = autos_origin[["origin_Europe", "origin_US"]].values
y_autos_origin = autos_origin['mpg'].values

X_train_autos_origin, X_test_autos_origin, y_train_autos_origin, y_test_autos_origin, = train_test_split(X_autos_origin,
                                                                                                         y_autos_origin, 
                                                                                                         test_size=.3, 
                                                                                                         random_state=42)
ridge_autos_origin = Ridge(alpha=.5, normalize=True).fit(X_train_autos_origin, y_train_autos_origin)
ridge_autos_origin.score(X_test_autos_origin, y_test_autos_origin)

0.3241789154336545

Exploring categorical features

The Gapminder dataset that we worked with in previous section also contained a categorical 'Region' feature, which we dropped since we did not have the tools to deal with it. Now however, we do, so we have added it back in!

We will explore this feature. Boxplots are particularly useful for visualizing categorical features such as this.

gapminder.head()

	population	fertility	HIV	CO2	BMI_male	GDP	BMI_female	life	child_mortality
0	34811059.0	2.73	0.1	3.328945	24.59620	12314.0	129.9049	75.3	29.5
1	19842251.0	6.43	2.0	1.474353	22.25083	7103.0	130.1247	58.3	192.0
2	40381860.0	2.24	0.5	4.785170	27.50170	14646.0	118.8915	75.5	15.4
3	2975029.0	1.40	0.1	1.804106	25.35542	7383.0	132.8108	72.5	20.0
4	21370348.0	1.96	0.1	18.016313	27.56373	41312.0	117.3755	81.5	5.2

gapminder_2 = pd.read_csv("datasets/gapminder_2.csv")
gapminder_2.head()

	population	fertility	HIV	CO2	BMI_male	GDP	BMI_female	life	child_mortality	Region
0	34811059.0	2.73	0.1	3.328945	24.59620	12314.0	129.9049	75.3	29.5	Middle East & North Africa
1	19842251.0	6.43	2.0	1.474353	22.25083	7103.0	130.1247	58.3	192.0	Sub-Saharan Africa
2	40381860.0	2.24	0.5	4.785170	27.50170	14646.0	118.8915	75.5	15.4	America
3	2975029.0	1.40	0.1	1.804106	25.35542	7383.0	132.8108	72.5	20.0	Europe & Central Asia
4	21370348.0	1.96	0.1	18.016313	27.56373	41312.0	117.3755	81.5	5.2	East Asia & Pacific

# Create a boxplot of life expectancy per region
gapminder_2.boxplot("life", "Region", rot=60)

# Show the plot
plt.show()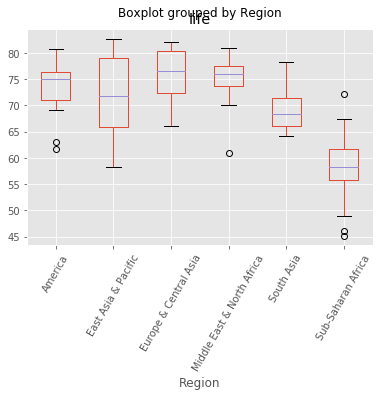

Important

Exploratory data analysis should always be the precursor to model building.

Creating dummy variables

scikit-learn does not accept non-numerical features. The 'Region' feature contains very useful information that can predict life expectancy. For example, Sub-Saharan Africa has a lower life expectancy compared to Europe and Central Asia. Therefore, if we are trying to predict life expectancy, it would be preferable to retain the 'Region' feature. To do this, we need to binarize it by creating dummy variables, which is what we will do.

# Create dummy variables with drop_first=True: df_region
gapminder_region = pd.get_dummies(gapminder_2, drop_first=True)

# Print the new columns of df_region
print(gapminder_region.columns)

Index(['population', 'fertility', 'HIV', 'CO2', 'BMI_male', 'GDP',
       'BMI_female', 'life', 'child_mortality', 'Region_East Asia & Pacific',
       'Region_Europe & Central Asia', 'Region_Middle East & North Africa',
       'Region_South Asia', 'Region_Sub-Saharan Africa'],
      dtype='object')

gapminder_region.head()

	population	fertility	HIV	CO2	BMI_male	GDP	BMI_female	life	child_mortality	Region_East Asia & Pacific	Region_Europe & Central Asia	Region_Middle East & North Africa	Region_Sub-Saharan Africa
0	34811059.0	2.73	0.1	3.328945	24.59620	12314.0	129.9049	75.3	29.5	0	0	1	0
1	19842251.0	6.43	2.0	1.474353	22.25083	7103.0	130.1247	58.3	192.0	0	0	0	1
2	40381860.0	2.24	0.5	4.785170	27.50170	14646.0	118.8915	75.5	15.4	0	0	0	0
3	2975029.0	1.40	0.1	1.804106	25.35542	7383.0	132.8108	72.5	20.0	0	1	0	0
4	21370348.0	1.96	0.1	18.016313	27.56373	41312.0	117.3755	81.5	5.2	1	0	0	0

Now that we have created the dummy variables, we can use the 'Region' feature to predict life expectancy!

Regression with categorical features

We’ll use ridge regression to perform 5-fold cross-validation.

X_gapminder_region = gapminder_region.drop("life", axis=1).values
y_gapminder_region = gapminder_region.life.values

# Instantiate a ridge regressor: ridge
ridge_gapminder_region = Ridge(alpha=.5, normalize=True)

# Perform 5-fold cross-validation: ridge_cv
ridge_cv_gapminder_region = cross_val_score(ridge_gapminder_region, X_gapminder_region, y_gapminder_region, cv=5)

# Print the cross-validated scores
print(ridge_cv_gapminder_region)

[0.86808336 0.80623545 0.84004203 0.7754344  0.87503712]

We now know how to build models using data that includes categorical features.

Handling missing data

Imputing missing data

Making an educated guess about the missing values

Example: Using the mean of the non-missing entries

PIMA Indians dataset

pidd.head()

	pregnancies	glucose	diastolic	triceps	insulin	bmi	dpf	age	diabetes
0	6	148	72	35.00000	155.548223	33.6	0.627	50	1
1	1	85	66	29.00000	155.548223	26.6	0.351	31	0
2	8	183	64	29.15342	155.548223	23.3	0.672	32	1
3	1	89	66	23.00000	94.000000	28.1	0.167	21	0
4	0	137	40	35.00000	168.000000	43.1	2.288	33	1

pidd.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   pregnancies  768 non-null    int64  
 1   glucose      768 non-null    int64  
 2   diastolic    768 non-null    int64  
 3   triceps      768 non-null    float64
 4   insulin      768 non-null    float64
 5   bmi          768 non-null    float64
 6   dpf          768 non-null    float64
 7   age          768 non-null    int64  
 8   diabetes     768 non-null    int64  
dtypes: float64(4), int64(5)
memory usage: 54.1 KB

pidd.insulin.replace(0, np.nan, inplace=True)
pidd.bmi.replace(0, np.nan, inplace=True)
pidd.triceps.replace(0, np.nan, inplace=True)
pidd.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   pregnancies  768 non-null    int64  
 1   glucose      768 non-null    int64  
 2   diastolic    768 non-null    int64  
 3   triceps      768 non-null    float64
 4   insulin      768 non-null    float64
 5   bmi          768 non-null    float64
 6   dpf          768 non-null    float64
 7   age          768 non-null    int64  
 8   diabetes     768 non-null    int64  
dtypes: float64(4), int64(5)
memory usage: 54.1 KB

pidd.head()

	pregnancies	glucose	diastolic	triceps	insulin	bmi	dpf	age	diabetes
0	6	148	72	35.00000	155.548223	33.6	0.627	50	1
1	1	85	66	29.00000	155.548223	26.6	0.351	31	0
2	8	183	64	29.15342	155.548223	23.3	0.672	32	1
3	1	89	66	23.00000	94.000000	28.1	0.167	21	0
4	0	137	40	35.00000	168.000000	43.1	2.288	33	1

Dropping missing data

The voting dataset1 contained a bunch of missing values that we dealt with for you behind the scenes.

votes2 = pd.read_csv("datasets/votes2.csv")
votes2.head()

	party	infants	water	budget	physician	salvador	religious	immigration	synfuels	education	superfund	crime	duty_free_exports	eaa_rsa
0	republican	0	1	0	1	1	1	1	?	1	1	1	0	1
1	republican	0	1	0	1	1	1	0	0	1	1	1	0	?
2	democrat	?	1	1	?	1	1	0	1	0	1	1	0	0
3	democrat	0	1	1	0	?	1	0	1	0	1	0	0	1
4	democrat	1	1	1	0	1	1	0	1	?	1	1	1	1

there are certain data points labeled with a '?'. These denote missing values. We will convert the '?'s to NaNs, and then drop the rows that contain them from the DataFrame.

# Convert '?' to NaN
votes2[votes2 == "?"] = np.nan

# Print the number of NaNs
display(votes2.isnull().sum())

# Print shape of original DataFrame
print("Shape of Original DataFrame: {}".format(votes2.shape))

# Print shape of new DataFrame
print("Shape of DataFrame After Dropping All Rows with Missing Values: {}".format(votes2.dropna().shape))

party                  0
infants               12
water                 48
budget                11
physician             11
salvador              15
religious             11
satellite             14
aid                   15
missile               22
immigration            7
synfuels              21
education             31
superfund             25
crime                 17
duty_free_exports     28
eaa_rsa              104
dtype: int64

Shape of Original DataFrame: (435, 17)
Shape of DataFrame After Dropping All Rows with Missing Values: (232, 17)

When many values in a dataset are missing, if you drop them, you may end up throwing away valuable information along with the missing data. It’s better instead to develop an imputation strategy. This is where domain knowledge is useful, but in the absence of it, you can impute missing values with the mean or the median of the row or column that the missing value is in.

Imputing missing data in a ML Pipeline I

there are many steps to building a model, from creating training and test sets, to fitting a classifier or regressor, to tuning its parameters, to evaluating its performance on new data. Imputation can be seen as the first step of this machine learning process, the entirety of which can be viewed within the context of a pipeline. Scikit-learn provides a pipeline constructor that allows you to piece together these steps into one process and thereby simplify your workflow.

We will be setting up a pipeline with two steps: the imputation step, followed by the instantiation of a classifier. We’ve seen three classifiers in this course so far: k-NN, logistic regression, and the decision tree. Here we will be using the SVM (Support Vector Machine)

votes2.head()

	party	infants	water	budget	physician	salvador	religious	immigration	synfuels	education	superfund	crime	duty_free_exports	eaa_rsa
0	republican	0	1	0	1	1	1	1	NaN	1	1	1	0	1
1	republican	0	1	0	1	1	1	0	0	1	1	1	0	NaN
2	democrat	NaN	1	1	NaN	1	1	0	1	0	1	1	0	0
3	democrat	0	1	1	0	NaN	1	0	1	0	1	0	0	1
4	democrat	1	1	1	0	1	1	0	1	NaN	1	1	1	1

votes2.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 435 entries, 0 to 434
Data columns (total 17 columns):
 #   Column             Non-Null Count  Dtype 
---  ------             --------------  ----- 
 0   party              435 non-null    object
 1   infants            423 non-null    object
 2   water              387 non-null    object
 3   budget             424 non-null    object
 4   physician          424 non-null    object
 5   salvador           420 non-null    object
 6   religious          424 non-null    object
 7   satellite          421 non-null    object
 8   aid                420 non-null    object
 9   missile            413 non-null    object
 10  immigration        428 non-null    object
 11  synfuels           414 non-null    object
 12  education          404 non-null    object
 13  superfund          410 non-null    object
 14  crime              418 non-null    object
 15  duty_free_exports  407 non-null    object
 16  eaa_rsa            331 non-null    object
dtypes: object(17)
memory usage: 57.9+ KB

# Setup the Imputation transformer: imp
imp_votes = SimpleImputer(missing_values=np.nan, strategy="most_frequent")

# Instantiate the SVC classifier: clf
clf_votes = SVC()

# Setup the pipeline with the required steps: steps
steps_votes = [('imputation', imp_votes),
        ('SVM', clf_votes)]

Having set up the pipeline steps, we can now use it for classification.

Imputing missing data in a ML Pipeline II

Having setup the steps of the pipeline we will now use it on the voting dataset to classify a Congressman’s party affiliation. What makes pipelines so incredibly useful is the simple interface that they provide.

X_votes[:5]

array([[0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1],
       [0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1],
       [0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0],
       [0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1],
       [1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1]], dtype=int64)

votes.head()

	party	infants	water	budget	physician	salvador	religious	immigration	synfuels	education	superfund	crime	duty_free_exports	eaa_rsa
0	republican	0	1	0	1	1	1	1	0	1	1	1	0	1
1	republican	0	1	0	1	1	1	0	0	1	1	1	0	1
2	democrat	0	1	1	0	1	1	0	1	0	1	1	0	0
3	democrat	0	1	1	0	1	1	0	1	0	1	0	0	1
4	democrat	1	1	1	0	1	1	0	1	0	1	1	1	1

X_votes = votes.drop("party", axis=1)
y_votes = votes.party

X_train_votes, X_test_votes, y_train_votes, y_test_votes = train_test_split(X_votes, y_votes, test_size=.3, random_state=42)

# Create the pipeline: pipeline
pipeline_votes = Pipeline(steps_votes)

# Fit the pipeline to the train set
pipeline_votes.fit(X_train_votes, y_train_votes)

# Predict the labels of the test set
y_pred_votes = pipeline_votes.predict(X_test_votes)

# Compute metrics
print(classification_report(y_test_votes, y_pred_votes))

              precision    recall  f1-score   support

    democrat       0.98      0.96      0.97        85
  republican       0.94      0.96      0.95        46

    accuracy                           0.96       131
   macro avg       0.96      0.96      0.96       131
weighted avg       0.96      0.96      0.96       131

Centering and scaling

Why scale your data?

Many models use some form of distance to inform them

Features on larger scales can unduly influence the model

Example: k-NN uses distance explicitly when making predictions

We want features to be on a similar scale

Normalizing (or scaling and centering)

Ways to normalize your data

Standardization: Subtract the mean and divide by variance

All features are centered around zero and have variance one

Can also subtract the minimum and divide by the range

Minimum zero and maximum one

Can also normalize so the data ranges from -1 to +1

Centering and scaling your data

the performance of a model can improve if the features are scaled. Note that this is not always the case: In the Congressional voting records dataset, for example, all of the features are binary. In such a situation, scaling will have minimal impact. We will explore scalling on White Wine Quality.

wwq = pd.read_csv("datasets/white_wine_quality.csv")
wwq.head()

	fixed acidity	volatile acidity	citric acid	residual sugar	chlorides	free sulfur dioxide	total sulfur dioxide	density	pH	sulphates	alcohol	quality
0	7.0	0.27	0.36	20.7	0.045	45.0	170.0	1.0010	3.00	0.45	8.8	6
1	6.3	0.30	0.34	1.6	0.049	14.0	132.0	0.9940	3.30	0.49	9.5	6
2	8.1	0.28	0.40	6.9	0.050	30.0	97.0	0.9951	3.26	0.44	10.1	6
3	7.2	0.23	0.32	8.5	0.058	47.0	186.0	0.9956	3.19	0.40	9.9	6
4	7.2	0.23	0.32	8.5	0.058	47.0	186.0	0.9956	3.19	0.40	9.9	6

X_wwq = pd.read_csv("datasets/X_wwq.csv").values
X_wwq[:5]

array([[7.000e+00, 2.700e-01, 3.600e-01, 2.070e+01, 4.500e-02, 4.500e+01,
        1.700e+02, 1.001e+00, 3.000e+00, 4.500e-01, 8.800e+00],
       [6.300e+00, 3.000e-01, 3.400e-01, 1.600e+00, 4.900e-02, 1.400e+01,
        1.320e+02, 9.940e-01, 3.300e+00, 4.900e-01, 9.500e+00],
       [8.100e+00, 2.800e-01, 4.000e-01, 6.900e+00, 5.000e-02, 3.000e+01,
        9.700e+01, 9.951e-01, 3.260e+00, 4.400e-01, 1.010e+01],
       [7.200e+00, 2.300e-01, 3.200e-01, 8.500e+00, 5.800e-02, 4.700e+01,
        1.860e+02, 9.956e-01, 3.190e+00, 4.000e-01, 9.900e+00],
       [7.200e+00, 2.300e-01, 3.200e-01, 8.500e+00, 5.800e-02, 4.700e+01,
        1.860e+02, 9.956e-01, 3.190e+00, 4.000e-01, 9.900e+00]])

y_wwq = np.array([False, False, False, False, False, False, False, False, False,
       False,  True,  True,  True, False,  True, False, False, False,
       False,  True, False, False, False,  True, False, False, False,
       False, False, False, False, False, False, False,  True,  True,
        True, False,  True,  True, False, False, False, False, False,
       False,  True,  True, False,  True, False, False, False, False,
       False, False, False, False, False, False, False, False,  True,
       False, False,  True, False,  True, False,  True, False,  True,
        True, False, False,  True, False, False,  True,  True, False,
       False,  True, False,  True, False, False, False,  True, False,
       False,  True, False, False, False, False, False, False,  True,
       False,  True,  True,  True,  True,  True, False,  True, False,
       False,  True, False,  True,  True,  True,  True,  True, False,
       False,  True,  True,  True,  True,  True, False, False, False,
        True, False, False, False,  True, False,  True,  True,  True,
        True, False,  True, False, False,  True,  True, False, False,
       False, False, False,  True, False, False, False, False, False,
        True, False, False, False, False, False, False, False,  True,
        True, False,  True,  True, False, False,  True,  True, False,
       False,  True, False,  True, False,  True,  True,  True, False,
       False,  True,  True, False,  True,  True, False,  True, False,
        True, False,  True, False,  True,  True, False,  True,  True,
        True,  True,  True,  True,  True, False,  True,  True,  True,
        True,  True, False,  True, False,  True, False, False,  True,
        True,  True,  True,  True,  True, False, False, False, False,
        True, False, False, False,  True,  True, False, False, False,
       False, False, False, False, False, False,  True,  True, False,
       False,  True, False, False, False, False,  True,  True,  True,
        True,  True, False, False, False, False, False,  True, False,
        True,  True, False, False,  True, False,  True, False, False,
       False,  True,  True,  True,  True, False, False,  True,  True,
       False, False, False,  True,  True,  True,  True, False, False,
       False, False, False, False,  True, False,  True, False,  True,
       False, False, False, False, False, False, False, False, False,
        True, False, False, False, False, False, False, False,  True,
       False, False,  True, False, False, False,  True, False, False,
        True,  True, False, False, False,  True, False,  True, False,
        True,  True, False, False, False,  True, False, False, False,
       False,  True, False, False, False, False, False,  True, False,
       False, False, False, False, False, False, False, False, False,
       False,  True, False, False, False, False, False, False, False,
        True, False, False,  True, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
        True, False, False, False,  True, False, False,  True,  True,
        True, False,  True, False, False,  True,  True,  True, False,
        True, False,  True, False,  True, False, False,  True,  True,
       False, False, False,  True, False, False, False, False, False,
       False, False, False, False,  True,  True,  True,  True,  True,
       False,  True, False, False,  True, False, False,  True, False,
       False, False, False, False,  True,  True, False, False, False,
        True,  True, False, False, False, False, False,  True, False,
        True,  True,  True,  True, False,  True,  True, False, False,
        True,  True, False,  True, False, False, False,  True, False,
       False, False, False,  True, False,  True,  True,  True, False,
       False, False, False, False, False, False, False, False, False,
       False,  True, False,  True,  True, False, False, False,  True,
       False, False,  True, False, False, False, False, False, False,
       False, False, False,  True, False, False,  True,  True,  True,
       False, False,  True, False,  True, False, False, False, False,
        True, False, False, False,  True,  True, False,  True, False,
        True,  True, False, False, False, False, False, False, False,
        True, False, False, False, False, False, False,  True, False,
        True, False, False,  True, False, False,  True, False, False,
        True, False, False,  True, False,  True, False, False, False,
       False, False, False, False,  True,  True, False, False, False,
       False, False, False, False, False,  True, False,  True,  True,
        True, False,  True, False, False, False, False, False,  True,
        True, False, False,  True,  True,  True, False, False, False,
        True,  True,  True,  True, False, False, False, False,  True,
        True, False,  True,  True, False,  True, False, False, False,
        True,  True, False,  True, False, False, False,  True,  True,
        True, False,  True, False,  True,  True,  True,  True, False,
        True, False, False, False, False, False, False, False, False,
        True,  True,  True,  True, False,  True,  True, False,  True,
       False, False, False,  True, False, False, False, False,  True,
       False, False, False, False, False,  True,  True, False,  True,
        True,  True, False,  True, False, False,  True, False,  True,
        True, False,  True, False,  True,  True,  True,  True, False,
        True, False, False,  True,  True, False, False,  True,  True,
       False, False,  True, False, False, False,  True, False, False,
        True,  True, False, False, False,  True, False,  True,  True,
        True, False, False, False, False,  True, False, False,  True,
       False, False,  True, False, False,  True,  True, False, False,
       False, False, False, False, False, False, False,  True, False,
        True, False, False, False, False, False,  True, False, False,
       False,  True, False, False, False, False, False, False,  True,
       False, False, False,  True, False, False,  True, False, False,
       False,  True, False, False, False, False, False, False, False,
        True, False,  True,  True, False, False, False, False, False,
        True,  True, False, False, False,  True, False, False, False,
        True, False, False, False, False,  True,  True,  True,  True,
        True, False, False,  True, False,  True, False, False, False,
       False, False, False,  True, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
        True,  True, False, False, False,  True, False,  True, False,
       False,  True,  True, False,  True, False, False, False, False,
        True, False, False, False, False, False,  True,  True, False,
        True,  True, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False,  True, False, False, False, False, False, False, False,
       False, False,  True, False, False,  True,  True, False,  True,
        True,  True,  True,  True,  True,  True,  True, False, False,
       False, False, False, False, False, False, False,  True,  True,
       False,  True,  True, False,  True, False,  True,  True,  True,
        True,  True, False, False,  True, False, False, False, False,
       False,  True,  True,  True,  True,  True, False, False,  True,
       False,  True,  True, False, False, False, False, False, False,
       False, False,  True, False, False, False, False, False, False,
       False, False, False,  True, False,  True, False,  True, False,
       False, False, False,  True, False, False, False,  True, False,
       False,  True,  True,  True, False, False,  True, False, False,
       False, False,  True, False, False, False, False, False,  True,
       False, False, False, False, False,  True,  True,  True,  True,
       False, False, False, False, False, False, False, False, False,
       False,  True, False,  True, False, False, False, False,  True,
       False,  True,  True, False,  True,  True,  True,  True,  True,
       False,  True,  True,  True,  True, False,  True, False,  True,
        True,  True,  True, False,  True, False,  True, False,  True,
        True,  True, False,  True, False, False, False, False, False,
        True, False,  True, False, False, False,  True,  True, False,
       False, False, False, False, False,  True, False, False, False,
       False, False, False, False, False,  True, False, False, False,
       False, False, False, False,  True,  True,  True, False, False,
       False, False,  True, False, False, False,  True,  True, False,
        True,  True,  True,  True, False, False, False,  True,  True,
       False, False, False,  True, False, False, False,  True,  True,
        True, False, False, False,  True,  True, False,  True,  True,
        True,  True,  True,  True,  True, False,  True,  True,  True,
        True, False,  True,  True, False, False, False, False, False,
       False, False, False, False,  True,  True, False,  True, False,
       False,  True, False,  True, False,  True, False, False,  True,
        True,  True, False,  True, False, False,  True,  True, False,
       False,  True, False, False, False, False, False, False, False,
       False, False, False, False, False,  True, False, False,  True,
       False,  True, False, False, False,  True, False, False, False,
        True, False,  True, False, False, False, False, False,  True,
       False, False, False,  True, False,  True, False, False, False,
       False, False,  True, False,  True, False,  True, False, False,
       False, False,  True,  True, False, False, False,  True, False,
        True, False, False,  True, False, False, False, False, False,
       False, False, False, False,  True, False, False, False,  True,
       False, False,  True,  True,  True, False, False, False,  True,
       False, False, False, False,  True, False, False, False, False,
       False, False, False, False, False, False,  True,  True, False,
       False, False, False,  True, False,  True, False, False,  True,
       False, False,  True, False, False, False, False,  True,  True,
       False, False, False,  True, False,  True, False, False, False,
        True, False, False, False, False, False,  True,  True, False,
       False, False, False, False, False,  True,  True, False, False,
        True, False, False, False, False, False, False, False,  True,
       False, False, False,  True,  True,  True, False, False, False,
       False, False, False, False,  True,  True, False, False,  True,
       False,  True, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False,  True,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
        True,  True, False, False, False, False, False, False, False,
       False, False,  True, False,  True,  True, False,  True, False,
        True,  True, False, False, False,  True, False,  True,  True,
        True, False, False,  True,  True,  True, False,  True,  True,
        True,  True,  True, False, False, False, False, False, False,
       False, False,  True, False, False,  True,  True, False, False,
       False, False, False, False, False, False, False,  True, False,
       False,  True,  True, False, False,  True, False,  True, False,
        True, False, False, False, False, False, False,  True,  True,
       False, False, False, False,  True, False,  True,  True, False,
       False, False,  True, False, False, False, False,  True,  True,
       False, False, False, False, False, False,  True,  True, False,
       False, False, False, False, False, False, False,  True, False,
        True,  True, False, False,  True, False, False, False, False,
        True, False, False, False, False, False,  True, False, False,
       False, False,  True, False, False,  True, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False,  True,  True, False,  True, False, False,  True, False,
        True,  True, False,  True,  True, False, False,  True,  True,
       False, False,  True,  True,  True,  True, False, False,  True,
       False,  True,  True, False,  True, False, False, False, False,
       False, False, False,  True, False, False, False, False, False,
        True, False,  True, False, False, False,  True, False, False,
       False, False, False,  True, False, False, False, False, False,
       False,  True, False, False, False, False, False,  True, False,
       False,  True, False, False, False, False, False,  True, False,
        True,  True,  True, False, False, False, False, False, False,
       False,  True,  True, False, False,  True, False,  True,  True,
        True, False,  True,  True, False, False, False, False,  True,
       False,  True, False, False, False, False, False,  True,  True,
       False,  True, False, False, False,  True,  True, False, False,
       False, False, False,  True, False,  True, False,  True, False,
       False,  True, False, False, False, False, False, False, False,
        True,  True,  True,  True, False, False,  True,  True,  True,
        True,  True, False, False,  True, False, False, False,  True,
       False, False, False, False, False, False, False, False, False,
        True, False, False, False,  True, False, False, False,  True,
       False,  True,  True, False, False, False, False,  True,  True,
        True, False,  True, False, False, False, False, False, False,
       False,  True,  True,  True,  True, False, False, False, False,
        True,  True,  True,  True,  True, False, False, False, False,
       False, False, False,  True, False, False, False,  True,  True,
       False, False, False, False, False, False,  True, False,  True,
        True, False,  True,  True, False,  True, False, False, False,
       False,  True, False, False, False,  True,  True, False,  True,
       False, False,  True, False, False, False, False, False,  True,
       False, False, False,  True, False, False,  True,  True,  True,
       False, False, False, False, False, False, False, False,  True,
       False, False, False, False,  True, False, False, False, False,
        True,  True,  True,  True, False, False, False, False,  True,
       False, False,  True,  True,  True, False, False, False, False,
        True, False, False, False, False, False, False, False, False,
        True,  True,  True,  True, False, False, False, False,  True,
       False,  True,  True,  True, False,  True,  True,  True,  True,
        True,  True,  True,  True,  True, False, False, False, False,
       False, False,  True, False,  True, False, False,  True, False,
       False,  True,  True, False, False, False, False, False,  True,
       False, False, False, False,  True,  True,  True,  True, False,
       False,  True, False,  True, False,  True, False,  True, False,
        True, False, False,  True,  True,  True,  True,  True,  True,
        True, False, False,  True, False,  True,  True,  True, False,
       False,  True,  True,  True, False, False,  True,  True,  True,
        True, False,  True, False, False, False, False, False, False,
       False,  True,  True,  True, False,  True, False, False, False,
       False, False, False, False, False, False, False,  True, False,
       False,  True, False,  True, False, False, False, False, False,
       False, False,  True,  True, False, False, False, False, False,
       False,  True, False, False,  True,  True, False,  True, False,
       False,  True, False, False, False, False, False, False,  True,
        True,  True,  True, False, False, False,  True, False,  True,
        True,  True, False,  True,  True,  True, False,  True, False,
       False, False,  True,  True,  True,  True, False,  True,  True,
        True,  True,  True, False,  True, False,  True,  True,  True,
       False,  True,  True, False,  True,  True,  True, False, False,
       False, False,  True,  True, False,  True,  True, False, False,
        True,  True,  True, False,  True, False, False,  True, False,
       False, False,  True,  True,  True,  True,  True,  True,  True,
        True, False,  True,  True, False,  True,  True,  True,  True,
        True, False, False, False,  True,  True,  True,  True, False,
        True,  True,  True, False,  True,  True, False,  True,  True,
       False,  True,  True,  True, False,  True,  True, False, False,
       False, False,  True, False,  True,  True,  True,  True,  True,
        True, False, False, False, False,  True,  True, False, False,
        True, False, False,  True,  True,  True, False, False,  True,
       False, False, False, False,  True,  True,  True, False, False,
       False, False, False,  True,  True, False, False,  True, False,
        True, False, False, False,  True,  True, False, False,  True,
        True, False, False, False,  True, False, False, False,  True,
       False, False,  True, False,  True, False,  True,  True,  True,
        True, False, False,  True, False, False, False, False, False,
        True, False,  True, False, False, False, False, False, False,
       False, False,  True,  True,  True, False, False, False, False,
       False,  True,  True, False,  True,  True, False, False,  True,
        True,  True,  True,  True, False,  True, False, False,  True,
       False, False,  True,  True, False, False,  True, False,  True,
       False,  True, False, False,  True, False,  True,  True, False,
       False, False, False, False, False,  True, False,  True, False,
       False, False,  True, False, False,  True,  True,  True,  True,
        True,  True,  True, False, False, False, False, False, False,
       False, False, False, False, False, False,  True,  True,  True,
       False, False,  True,  True,  True, False,  True, False,  True,
       False, False, False, False,  True,  True, False, False,  True,
       False, False,  True, False,  True, False,  True,  True, False,
        True, False, False,  True,  True,  True,  True,  True, False,
       False,  True, False,  True, False, False,  True, False, False,
        True,  True, False, False, False, False, False, False,  True,
        True,  True, False,  True, False,  True,  True,  True,  True,
       False, False, False, False,  True,  True,  True, False, False,
       False, False,  True,  True,  True, False, False, False, False,
        True,  True,  True,  True, False, False, False, False, False,
        True,  True,  True, False, False, False,  True,  True, False,
       False,  True,  True, False, False,  True,  True, False, False,
        True,  True,  True,  True, False,  True,  True,  True, False,
        True,  True, False,  True, False, False, False, False, False,
        True,  True,  True, False, False,  True,  True, False,  True,
       False,  True, False,  True,  True,  True,  True,  True, False,
       False, False,  True,  True, False, False,  True, False, False,
       False, False,  True,  True,  True,  True, False,  True,  True,
        True, False, False,  True,  True, False, False, False, False,
        True, False, False, False, False,  True, False, False, False,
        True, False,  True, False, False, False, False,  True, False,
        True,  True,  True,  True,  True,  True, False,  True,  True,
        True,  True, False, False, False, False, False,  True, False,
       False, False,  True, False, False, False, False, False,  True,
        True, False, False,  True,  True, False, False, False, False,
        True, False,  True,  True,  True, False, False, False, False,
       False,  True,  True, False,  True, False, False, False,  True,
        True, False,  True,  True, False,  True, False, False, False,
        True, False, False,  True, False,  True, False,  True, False,
        True, False,  True, False, False,  True, False,  True,  True,
        True, False,  True,  True, False, False,  True, False, False,
       False, False, False, False, False, False,  True, False, False,
        True,  True, False,  True,  True, False,  True, False, False,
        True, False, False, False, False, False, False, False, False,
        True,  True, False,  True,  True, False, False, False, False,
       False,  True,  True, False, False,  True,  True, False, False,
       False,  True, False, False,  True,  True,  True, False,  True,
        True, False, False, False,  True,  True,  True, False, False,
       False,  True, False, False,  True,  True, False,  True,  True,
        True,  True, False, False, False, False, False, False, False,
       False,  True, False, False, False,  True, False, False, False,
       False, False, False, False, False,  True, False, False, False,
       False,  True, False, False, False,  True, False, False, False,
       False, False, False, False, False, False,  True, False, False,
       False,  True,  True,  True, False, False, False,  True, False,
        True,  True,  True,  True, False, False, False,  True, False,
       False, False, False,  True, False, False, False,  True, False,
       False, False, False,  True,  True,  True, False, False, False,
       False, False,  True, False, False,  True, False, False, False,
       False, False, False, False, False, False, False, False, False,
        True,  True, False,  True, False, False, False,  True,  True,
       False, False, False, False, False, False,  True, False, False,
       False, False, False, False, False, False, False,  True,  True,
       False, False, False, False,  True, False,  True,  True,  True,
       False,  True,  True, False,  True, False, False,  True, False,
       False,  True,  True, False, False, False, False,  True,  True,
       False, False, False,  True, False, False, False,  True,  True,
       False,  True, False,  True,  True,  True, False, False, False,
       False, False, False,  True,  True,  True, False, False, False,
       False, False, False, False, False, False, False, False, False,
        True, False, False,  True,  True,  True,  True,  True,  True,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False,  True, False, False,
       False, False, False, False, False,  True,  True, False, False,
        True, False,  True, False, False, False,  True,  True,  True,
       False, False, False,  True, False, False,  True,  True,  True,
        True,  True, False, False,  True, False, False,  True,  True,
       False, False, False,  True,  True, False,  True, False, False,
       False, False, False,  True,  True, False, False, False, False,
        True, False, False, False, False, False, False, False, False,
        True,  True,  True,  True, False, False, False,  True,  True,
       False, False, False, False, False, False, False,  True,  True,
        True,  True, False,  True, False, False,  True, False, False,
       False,  True, False,  True, False, False, False,  True, False,
        True,  True, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False,  True, False, False, False, False,
       False, False, False, False, False, False,  True,  True, False,
       False, False, False,  True, False, False, False, False,  True,
       False, False, False,  True, False, False, False,  True, False,
       False, False, False, False, False,  True, False,  True,  True,
        True, False,  True, False, False,  True,  True,  True, False,
        True,  True, False,  True,  True, False,  True,  True, False,
       False, False, False, False,  True,  True, False,  True,  True,
        True,  True, False,  True, False, False, False, False, False,
        True, False, False, False, False, False, False, False, False,
       False,  True, False, False, False, False, False, False,  True,
       False, False, False,  True,  True, False, False,  True, False,
       False, False, False, False, False,  True, False,  True, False,
        True, False,  True, False,  True, False, False, False,  True,
       False, False, False, False,  True, False, False, False, False,
       False, False,  True, False, False, False, False, False, False,
       False, False, False, False, False, False,  True, False, False,
       False, False,  True, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
        True, False,  True, False, False,  True, False, False, False,
        True, False, False,  True, False, False, False,  True,  True,
       False, False, False, False, False, False, False, False, False,
        True, False, False, False,  True,  True,  True, False,  True,
       False, False, False,  True,  True,  True, False,  True, False,
       False, False, False, False, False, False, False, False, False,
       False,  True, False, False, False, False, False,  True, False,
       False, False, False, False, False,  True, False, False, False,
       False, False, False, False, False,  True, False, False, False,
       False, False, False,  True, False, False, False,  True, False,
       False, False,  True,  True, False, False, False,  True,  True,
       False, False,  True, False,  True, False, False, False, False,
       False, False, False, False,  True,  True, False,  True, False,
       False,  True,  True,  True, False, False,  True, False, False,
       False, False, False, False,  True, False, False, False, False,
       False, False, False, False, False, False, False,  True,  True,
       False, False, False, False, False,  True, False,  True, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False,  True, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False,  True,
       False, False, False, False,  True, False, False, False, False,
       False, False, False,  True, False, False, False, False, False,
       False,  True,  True, False, False,  True, False, False,  True,
       False,  True, False, False, False,  True, False,  True, False,
       False, False, False, False, False, False,  True, False, False,
        True, False, False,  True, False, False, False, False, False,
        True, False, False,  True, False, False, False, False,  True,
        True,  True,  True,  True, False, False,  True, False, False,
       False, False, False, False, False,  True, False,  True, False,
        True, False, False, False, False, False, False, False,  True,
       False, False,  True, False, False, False, False, False, False,
       False, False, False, False, False, False, False,  True, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False,  True, False, False, False, False, False,  True, False,
       False, False, False, False, False, False, False, False,  True,
       False,  True, False,  True,  True, False, False, False, False,
        True, False,  True,  True, False, False,  True,  True, False,
        True, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False,  True, False,  True, False,  True,
       False, False, False, False, False, False, False,  True, False,
       False, False, False,  True, False,  True, False,  True, False,
       False, False, False, False, False, False, False, False, False,
        True, False, False, False, False, False, False, False, False,
       False, False, False, False, False,  True,  True, False, False,
       False,  True, False, False, False,  True, False,  True,  True,
       False, False, False, False, False, False, False,  True,  True,
        True, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False,  True, False,  True, False, False, False,
       False, False, False, False, False, False, False, False,  True,
       False, False, False, False, False,  True, False, False, False,
       False, False,  True, False, False, False,  True, False, False,
       False, False, False, False, False,  True,  True, False, False,
       False, False, False, False,  True, False, False, False, False,
        True,  True,  True, False, False, False, False, False, False,
        True,  True,  True, False,  True,  True,  True, False,  True,
       False,  True,  True, False,  True,  True, False, False, False,
       False, False, False,  True, False, False,  True, False,  True,
       False,  True,  True, False, False, False, False, False, False,
       False, False,  True, False,  True, False, False,  True,  True,
        True, False, False,  True,  True,  True, False, False, False,
        True,  True, False,  True,  True,  True, False,  True,  True,
       False, False,  True,  True, False,  True, False, False, False,
        True, False, False,  True, False, False,  True,  True,  True,
       False,  True,  True, False, False,  True, False, False,  True,
        True,  True,  True, False,  True, False,  True, False,  True,
        True, False, False,  True,  True,  True,  True,  True, False,
        True, False, False, False,  True, False, False,  True, False,
       False, False,  True, False, False, False,  True,  True, False,
        True,  True, False, False,  True,  True, False, False, False,
       False, False,  True, False,  True, False,  True, False, False,
       False, False, False, False, False, False, False,  True,  True,
       False, False, False, False, False, False,  True, False, False,
       False, False,  True,  True,  True, False,  True,  True,  True,
        True, False, False,  True, False, False, False, False, False,
       False, False, False,  True,  True,  True, False, False, False,
       False, False,  True,  True,  True, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False,  True, False, False, False,  True, False,  True,
        True,  True, False,  True,  True,  True, False, False, False,
        True, False,  True, False,  True, False, False,  True,  True,
       False, False, False, False, False, False,  True,  True,  True,
        True, False, False,  True, False,  True,  True, False, False,
       False,  True, False, False,  True,  True, False,  True, False,
       False, False, False, False,  True, False, False, False, False,
       False, False,  True, False, False, False, False, False, False,
       False, False, False, False,  True, False, False, False,  True,
       False, False, False, False, False,  True, False, False, False,
       False, False,  True, False, False, False, False, False, False,
       False,  True,  True, False, False,  True,  True,  True,  True,
       False, False, False, False,  True, False, False,  True,  True,
        True, False,  True, False,  True,  True,  True,  True,  True,
        True, False, False, False, False, False, False, False, False,
       False, False,  True, False, False, False,  True, False, False,
       False,  True,  True, False,  True,  True, False, False,  True,
       False, False,  True, False, False,  True,  True, False,  True,
       False, False, False, False, False, False,  True, False, False,
       False, False, False, False, False, False, False, False, False,
       False,  True, False,  True, False, False,  True,  True, False,
       False, False,  True, False, False, False,  True, False, False,
       False, False, False, False, False, False, False,  True, False,
       False, False, False,  True,  True,  True,  True, False, False,
        True,  True, False, False,  True, False,  True, False, False,
       False, False, False, False, False, False, False, False, False,
       False,  True, False, False,  True,  True,  True,  True, False,
       False, False, False, False, False,  True,  True, False, False,
       False, False, False, False,  True, False,  True, False, False,
       False, False, False,  True, False, False, False, False, False,
        True,  True, False, False,  True, False,  True, False, False,
       False, False, False,  True,  True, False, False, False, False,
        True, False, False, False, False, False, False, False, False,
        True,  True,  True,  True,  True,  True, False,  True, False,
       False,  True,  True, False,  True, False, False, False, False,
       False, False, False, False, False,  True,  True,  True,  True,
       False, False, False, False, False,  True,  True, False, False,
       False, False, False, False, False,  True,  True,  True,  True,
        True, False, False, False, False, False, False, False, False,
       False, False, False,  True, False,  True, False, False, False,
       False, False,  True,  True, False, False,  True,  True, False,
       False, False, False,  True, False, False,  True,  True, False,
        True,  True,  True, False, False, False, False,  True,  True,
       False, False, False, False, False, False, False, False, False,
        True, False, False, False, False,  True, False, False, False,
        True, False, False, False, False,  True,  True,  True,  True,
        True,  True,  True, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False,  True, False, False,  True, False, False, False,
        True, False,  True, False,  True, False, False,  True, False,
        True, False,  True, False, False,  True,  True, False, False,
        True, False,  True, False,  True,  True, False, False, False,
       False,  True,  True, False, False, False,  True,  True,  True,
        True, False, False,  True,  True,  True,  True,  True,  True,
       False, False,  True,  True,  True, False, False,  True, False,
        True, False, False, False, False,  True,  True, False, False,
       False, False, False, False, False, False, False, False,  True,
       False, False,  True, False, False,  True, False, False, False,
       False,  True,  True,  True, False,  True,  True, False, False,
       False, False,  True, False, False,  True,  True, False, False,
        True,  True,  True, False,  True, False, False, False, False,
        True,  True,  True,  True, False, False, False, False,  True,
        True, False, False, False,  True,  True,  True,  True,  True,
       False,  True,  True, False, False, False, False, False, False,
       False, False, False, False, False, False,  True,  True, False,
       False, False, False, False,  True,  True, False,  True,  True,
        True, False, False, False, False,  True, False, False, False,
       False, False,  True,  True, False,  True, False, False, False,
       False, False, False, False, False, False,  True, False, False,
       False,  True, False,  True, False, False,  True,  True, False,
       False, False, False,  True,  True, False, False, False, False,
       False,  True,  True, False, False, False, False, False, False,
       False, False,  True,  True,  True, False, False, False, False,
       False, False, False, False,  True, False, False, False, False,
       False, False, False, False, False, False, False,  True, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False,  True, False,
       False,  True, False,  True,  True,  True,  True, False,  True,
       False, False,  True, False, False, False, False, False,  True,
       False, False, False, False, False, False, False, False, False,
       False,  True, False,  True, False, False, False, False, False,
       False, False, False, False,  True,  True,  True, False,  True,
       False, False, False, False, False, False, False, False,  True,
       False, False, False, False,  True, False, False,  True, False,
        True,  True, False, False, False, False, False, False,  True,
        True, False, False, False, False,  True,  True, False, False,
       False, False, False,  True, False, False, False, False, False,
       False,  True,  True, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False,  True, False, False, False, False,
       False, False, False, False,  True,  True, False, False, False,
       False, False, False, False, False, False,  True, False, False,
        True,  True,  True, False, False,  True, False,  True, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False,  True, False,  True, False, False, False, False,
        True,  True,  True, False, False,  True, False, False, False,
        True, False, False, False, False, False,  True, False, False,
       False,  True, False, False, False, False, False,  True, False,
       False, False,  True, False,  True, False, False,  True, False,
       False, False, False, False, False,  True, False, False, False,
        True, False, False, False,  True, False, False, False,  True,
       False, False, False,  True, False, False,  True, False, False,
       False,  True, False,  True, False, False, False,  True, False,
        True,  True,  True, False, False, False, False,  True, False,
       False, False, False, False,  True, False, False, False, False,
       False, False, False,  True, False, False, False, False,  True,
        True, False, False, False,  True, False,  True, False, False,
       False,  True, False, False, False,  True, False,  True, False,
       False, False])

y_wwq = pd.read_csv("datasets/y_wwq.csv").values
y_wwq[:5]

array([[False],
       [False],
       [False],
       [False],
       [False]])

some features seem to have different units of measurement. 'density', for instance, takes values between 0.98 and 1.04, while 'total sulfur dioxide' ranges from 9 to 440. As a result, it may be worth scaling the features here. We will scale the features and compute the mean and standard deviation of the unscaled features compared to the scaled features.

# Scale the features: X_scaled
X_scaled_wwq = scale(X_wwq)

# Print the mean and standard deviation of the unscaled features
print("Mean of Unscaled Features: {}".format(np.mean(X_wwq))) 
print("Standard Deviation of Unscaled Features: {}".format(np.std(X_wwq)))

Mean of Unscaled Features: 18.43268707245592
Standard Deviation of Unscaled Features: 41.544947640946354

# Print the mean and standard deviation of the scaled features
print("Mean of Scaled Features: {}".format(np.mean(X_scaled_wwq))) 
print("Standard Deviation of Scaled Features: {}".format(np.std(X_scaled_wwq)))

Mean of Scaled Features: 2.660809650821445e-15
Standard Deviation of Scaled Features: 1.0

Centering and scaling in a pipeline

With regard to whether or not scaling is effective, the proof is in the pudding! We will See for ourselves whether or not scaling the features of the White Wine Quality dataset has any impact on its performance. We will use a k-NN classifier as part of a pipeline that includes scaling, and for the purposes of comparison

# Setup the pipeline steps: steps
steps_wwq = [('scaler', StandardScaler()),
        ('knn', KNeighborsClassifier())]
        
# Create the pipeline: pipeline
pipeline_wwq = Pipeline(steps_wwq)

# Create train and test sets
X_train_wwq, X_test_wwq, y_train_wwq, y_test_wwq = train_test_split(X_wwq,y_wwq, test_size=.3, random_state=42)

# Fit the pipeline to the training set: knn_scaled
knn_scaled_wwq = pipeline_wwq.fit(X_train_wwq, y_train_wwq)

# Instantiate and fit a k-NN classifier to the unscaled data
knn_unscaled_wwq = KNeighborsClassifier().fit(X_train_wwq, y_train_wwq)

# Compute and print metrics
print('Accuracy with Scaling: {}'.format(knn_scaled_wwq.score(X_test_wwq, y_test_wwq)))
print('Accuracy without Scaling: {}'.format(knn_unscaled_wwq.score(X_test_wwq, y_test_wwq)))

Accuracy with Scaling: 0.7700680272108843
Accuracy without Scaling: 0.6979591836734694

It looks like scaling has significantly improved model performance!

Bringing it all together I: Pipeline for classification

We will build a pipeline that includes scaling and hyperparameter tuning to classify wine quality.

X_wwq[:5]

array([[7.000e+00, 2.700e-01, 3.600e-01, 2.070e+01, 4.500e-02, 4.500e+01,
        1.700e+02, 1.001e+00, 3.000e+00, 4.500e-01, 8.800e+00],
       [6.300e+00, 3.000e-01, 3.400e-01, 1.600e+00, 4.900e-02, 1.400e+01,
        1.320e+02, 9.940e-01, 3.300e+00, 4.900e-01, 9.500e+00],
       [8.100e+00, 2.800e-01, 4.000e-01, 6.900e+00, 5.000e-02, 3.000e+01,
        9.700e+01, 9.951e-01, 3.260e+00, 4.400e-01, 1.010e+01],
       [7.200e+00, 2.300e-01, 3.200e-01, 8.500e+00, 5.800e-02, 4.700e+01,
        1.860e+02, 9.956e-01, 3.190e+00, 4.000e-01, 9.900e+00],
       [7.200e+00, 2.300e-01, 3.200e-01, 8.500e+00, 5.800e-02, 4.700e+01,
        1.860e+02, 9.956e-01, 3.190e+00, 4.000e-01, 9.900e+00]])

# Setup the pipeline
steps_wwq = [('scaler', StandardScaler()),
         ('SVM', SVC())]

pipeline_wwq = Pipeline(steps_wwq)

# Specify the hyperparameter space
parameters_wwq = {'SVM__C':[1, 10, 100],
              'SVM__gamma':[0.1, 0.01]}

# Create train and test sets
X_train_wwq, X_test_wwq, y_train_wwq, y_test_wwq = train_test_split(X_wwq,y_wwq, test_size=.2, random_state=21)

# Instantiate the GridSearchCV object: cv
cv_wwq = GridSearchCV(pipeline_wwq, param_grid=parameters_wwq, cv=3)

# Fit to the training set
cv_wwq.fit(X_train_wwq, y_train_wwq)

# Predict the labels of the test set: y_pred
y_pred_wwq = cv_wwq.predict(X_test_wwq)

# Compute and print metrics
print("Accuracy: {}".format(cv_wwq.score(X_test_wwq, y_test_wwq)))
print(classification_report(y_test_wwq, y_pred_wwq))
print("Tuned Model Parameters: {}".format(cv_wwq.best_params_))

Accuracy: 0.7795918367346939
              precision    recall  f1-score   support

       False       0.83      0.85      0.84       662
        True       0.67      0.63      0.65       318

    accuracy                           0.78       980
   macro avg       0.75      0.74      0.74       980
weighted avg       0.78      0.78      0.78       980

Tuned Model Parameters: {'SVM__C': 10, 'SVM__gamma': 0.1}

Bringing it all together II: Pipeline for regression

We will return to the gapminder dataset, it had a lot of missing data. We will build a pipeline that imputes the missing data, scales the features, and fits an ElasticNet to the Gapminder data. We will then tune the l1_ratio of the ElasticNet using GridSearchCV.

X_gapminder = np.array([[3.48110590e+07, 2.73000000e+00, 1.00000000e-01, 3.32894466e+00,
        2.45962000e+01, 1.23140000e+04, 1.29904900e+02, 2.95000000e+01],
       [1.98422510e+07, 6.43000000e+00, 2.00000000e+00, 1.47435339e+00,
        2.22508300e+01, 7.10300000e+03, 1.30124700e+02, 1.92000000e+02],
       [4.03818600e+07, 2.24000000e+00, 5.00000000e-01, 4.78516998e+00,
        2.75017000e+01, 1.46460000e+04, 1.18891500e+02, 1.54000000e+01],
       [2.97502900e+06, 1.40000000e+00, 1.00000000e-01, 1.80410622e+00,
        2.53554200e+01, 7.38300000e+03, 1.32810800e+02, 2.00000000e+01],
       [2.13703480e+07, 1.96000000e+00, 1.00000000e-01, 1.80163133e+01,
        2.75637300e+01, 4.13120000e+04, 1.17375500e+02, 5.20000000e+00],
       [8.33146500e+06, 1.41000000e+00, 3.00000000e-01, 8.18316002e+00,
        2.64674100e+01, 4.39520000e+04, 1.24139400e+02, 4.60000000e+00],
       [8.86871300e+06, 1.99000000e+00, 1.00000000e-01, 5.10953829e+00,
        2.56511700e+01, 1.43650000e+04, 1.28602400e+02, 4.33000000e+01],
       [3.48587000e+05, 1.89000000e+00, 3.10000000e+00, 3.13192132e+00,
        2.72459400e+01, 2.43730000e+04, 1.24386200e+02, 1.45000000e+01],
       [1.48252473e+08, 2.38000000e+00, 6.00000000e-02, 3.19161002e-01,
        2.03974200e+01, 2.26500000e+03, 1.25030700e+02, 5.59000000e+01],
       [2.77315000e+05, 1.83000000e+00, 1.30000000e+00, 6.00827884e+00,
        2.63843900e+01, 1.60750000e+04, 1.26394000e+02, 1.54000000e+01],
       [9.52645300e+06, 1.42000000e+00, 2.00000000e-01, 6.48817388e+00,
        2.61644300e+01, 1.44880000e+04, 1.29796800e+02, 7.20000000e+00],
       [1.07791550e+07, 1.82000000e+00, 2.00000000e-01, 9.79733671e+00,
        2.67591500e+01, 4.16410000e+04, 1.21822700e+02, 4.70000000e+00],
       [3.06165000e+05, 2.91000000e+00, 2.40000000e+00, 1.36012592e+00,
        2.70225500e+01, 8.29300000e+03, 1.20922400e+02, 2.01000000e+01],
       [8.97352500e+06, 5.27000000e+00, 1.20000000e+00, 5.37539184e-01,
        2.24183500e+01, 1.64600000e+03, 1.30272300e+02, 1.16300000e+02],
       [6.94990000e+05, 2.51000000e+00, 2.00000000e-01, 6.01210310e-01,
        2.28218000e+01, 5.66300000e+03, 1.25125800e+02, 4.81000000e+01],
       [9.59991600e+06, 3.48000000e+00, 2.00000000e-01, 1.43182915e+00,
        2.44333500e+01, 5.06600000e+03, 1.22415500e+02, 5.20000000e+01],
       [1.96786600e+06, 2.86000000e+00, 2.49000000e+01, 2.54720549e+00,
        2.21298400e+01, 1.38580000e+04, 1.33130700e+02, 6.38000000e+01],
       [1.94769696e+08, 1.90000000e+00, 4.50000000e-01, 2.02377284e+00,
        2.57862300e+01, 1.39060000e+04, 1.24874500e+02, 1.86000000e+01],
       [7.51364600e+06, 1.43000000e+00, 1.00000000e-01, 6.69013908e+00,
        2.65428600e+01, 1.53680000e+04, 1.28472100e+02, 1.37000000e+01],
       [1.47090110e+07, 6.04000000e+00, 1.20000000e+00, 1.09419171e-01,
        2.12715700e+01, 1.35800000e+03, 1.30665100e+02, 1.30400000e+02],
       [8.82179500e+06, 6.48000000e+00, 3.50000000e+00, 3.13888013e-02,
        2.15029100e+01, 7.23000000e+02, 1.34195500e+02, 1.08600000e+02],
       [1.39336600e+07, 3.05000000e+00, 6.00000000e-01, 2.87547496e-01,
        2.08049600e+01, 2.44200000e+03, 1.17552800e+02, 5.15000000e+01],
       [1.95704180e+07, 5.17000000e+00, 5.30000000e+00, 2.95541639e-01,
        2.36817300e+01, 2.57100000e+03, 1.27282300e+02, 1.13800000e+02],
       [3.33632560e+07, 1.68000000e+00, 2.00000000e-01, 1.63503986e+01,
        2.74521000e+01, 4.14680000e+04, 1.18057100e+02, 5.80000000e+00],
       [1.11397400e+07, 6.81000000e+00, 3.40000000e+00, 4.78391264e-02,
        2.14856900e+01, 1.75300000e+03, 1.27864000e+02, 1.68000000e+02],
       [1.66459400e+07, 1.89000000e+00, 4.00000000e-01, 4.24025914e+00,
        2.70154200e+01, 1.86980000e+04, 1.25541700e+02, 8.90000000e+00],
       [4.49016600e+07, 2.43000000e+00, 5.00000000e-01, 1.47609182e+00,
        2.49404100e+01, 1.04890000e+04, 1.24023500e+02, 1.97000000e+01],
       [6.65414000e+05, 5.05000000e+00, 6.00000000e-02, 1.78853064e-01,
        2.20613100e+01, 1.44000000e+03, 1.32135400e+02, 9.12000000e+01],
       [3.83277100e+06, 5.10000000e+00, 3.50000000e+00, 3.84220477e-01,
        2.18713400e+01, 5.02200000e+03, 1.31693500e+02, 7.26000000e+01],
       [4.42950600e+06, 1.91000000e+00, 3.00000000e-01, 1.91193342e+00,
        2.64789700e+01, 1.22190000e+04, 1.21350000e+02, 1.03000000e+01],
       [1.92616470e+07, 4.91000000e+00, 3.70000000e+00, 3.61896603e-01,
        2.25646900e+01, 2.85400000e+03, 1.31523700e+02, 1.16900000e+02],
       [4.34415100e+06, 1.43000000e+00, 6.00000000e-02, 5.28790258e+00,
        2.65962900e+01, 2.18730000e+04, 1.30392100e+02, 5.90000000e+00],
       [1.12902390e+07, 1.50000000e+00, 1.00000000e-01, 2.70177717e+00,
        2.50686700e+01, 1.77650000e+04, 1.26059400e+02, 6.30000000e+00],
       [5.49530200e+06, 1.89000000e+00, 2.00000000e-01, 8.54150780e+00,
        2.61328700e+01, 4.50170000e+04, 1.19581500e+02, 4.30000000e+00],
       [8.09639000e+05, 3.76000000e+00, 2.60000000e+00, 6.12799524e-01,
        2.33840300e+01, 2.50200000e+03, 1.29337600e+02, 8.10000000e+01],
       [1.44476000e+07, 2.73000000e+00, 4.00000000e-01, 2.11051780e+00,
        2.55884100e+01, 9.24400000e+03, 1.22986400e+02, 2.68000000e+01],
       [7.89761220e+07, 2.95000000e+00, 6.00000000e-02, 2.51239420e+00,
        2.67324300e+01, 9.97400000e+03, 1.25093100e+02, 3.14000000e+01],
       [6.00419900e+06, 2.32000000e+00, 8.00000000e-01, 1.06776463e+00,
        2.63675100e+01, 7.45000000e+03, 1.19932100e+02, 2.16000000e+01],
       [6.86223000e+05, 5.31000000e+00, 4.70000000e+00, 6.79825323e+00,
        2.37664000e+01, 4.01430000e+04, 1.32039200e+02, 1.18400000e+02],
       [4.50063800e+06, 5.16000000e+00, 8.00000000e-01, 8.37456442e-02,
        2.08850900e+01, 1.08800000e+03, 1.25794800e+02, 6.04000000e+01],
       [1.33994100e+06, 1.62000000e+00, 1.20000000e+00, 1.30313789e+01,
        2.62644600e+01, 2.47430000e+04, 1.29516100e+02, 5.50000000e+00],
       [8.43206000e+05, 2.74000000e+00, 1.00000000e-01, 1.27777956e+00,
        2.65307800e+01, 7.12900000e+03, 1.27476800e+02, 2.40000000e+01],
       [5.31417000e+06, 1.85000000e+00, 1.00000000e-01, 1.06441143e+01,
        2.67333900e+01, 4.21220000e+04, 1.26564500e+02, 3.30000000e+00],
       [6.23095290e+07, 1.97000000e+00, 4.00000000e-01, 5.99902073e+00,
        2.58532900e+01, 3.75050000e+04, 1.20014600e+02, 4.30000000e+00],
       [1.47374100e+06, 4.28000000e+00, 5.30000000e+00, 1.07953932e+00,
        2.40762000e+01, 1.58000000e+04, 1.30362500e+02, 6.80000000e+01],
       [1.58674900e+06, 5.80000000e+00, 1.70000000e+00, 2.51002328e-01,
        2.16502900e+01, 1.56600000e+03, 1.30208000e+02, 8.74000000e+01],
       [4.34329000e+06, 1.79000000e+00, 1.00000000e-01, 1.41942978e+00,
        2.55494200e+01, 5.90000000e+03, 1.30578900e+02, 1.93000000e+01],
       [8.06659060e+07, 1.37000000e+00, 1.00000000e-01, 9.49724676e+00,
        2.71650900e+01, 4.11990000e+04, 1.24904400e+02, 4.40000000e+00],
       [2.31159190e+07, 4.19000000e+00, 1.80000000e+00, 3.66600849e-01,
        2.28424700e+01, 2.90700000e+03, 1.28295300e+02, 7.99000000e+01],
       [1.11617550e+07, 1.46000000e+00, 1.00000000e-01, 8.66123553e+00,
        2.63378600e+01, 3.21970000e+04, 1.22934200e+02, 4.90000000e+00],
       [1.41066870e+07, 4.12000000e+00, 8.00000000e-01, 8.35594820e-01,
        2.52994700e+01, 6.96000000e+03, 1.20959600e+02, 3.69000000e+01],
       [1.04273560e+07, 5.34000000e+00, 1.40000000e+00, 1.26964400e-01,
        2.25244900e+01, 1.23000000e+03, 1.32276500e+02, 1.21000000e+02],
       [1.56129300e+06, 5.25000000e+00, 2.50000000e+00, 1.56376432e-01,
        2.16433800e+01, 1.32600000e+03, 1.30762700e+02, 1.27600000e+02],
       [7.48096000e+05, 2.74000000e+00, 1.20000000e+00, 2.07341531e+00,
        2.36846500e+01, 5.20800000e+03, 1.25151200e+02, 4.19000000e+01],
       [9.70513000e+06, 3.50000000e+00, 2.00000000e+00, 2.49306755e-01,
        2.36630200e+01, 1.60000000e+03, 1.25346100e+02, 8.33000000e+01],
       [7.25947000e+06, 3.27000000e+00, 8.00000000e-01, 1.18745352e+00,
        2.51087200e+01, 4.39100000e+03, 1.22962100e+02, 2.65000000e+01],
       [1.00506990e+07, 1.33000000e+00, 6.00000000e-02, 5.45323172e+00,
        2.71156800e+01, 2.33340000e+04, 1.28696800e+02, 7.20000000e+00],
       [3.10033000e+05, 2.12000000e+00, 3.00000000e-01, 6.82190305e+00,
        2.72068700e+01, 4.22940000e+04, 1.18738100e+02, 2.70000000e+00],
       [1.19707011e+09, 2.64000000e+00, 3.20000000e-01, 1.52084942e+00,
        2.09595600e+01, 3.90100000e+03, 1.23127400e+02, 6.56000000e+01],
       [2.35360765e+08, 2.48000000e+00, 2.00000000e-01, 1.75504422e+00,
        2.18557600e+01, 7.85600000e+03, 1.26421600e+02, 3.62000000e+01],
       [7.25306930e+07, 1.88000000e+00, 2.00000000e-01, 7.89221094e+00,
        2.53100300e+01, 1.59550000e+04, 1.25185900e+02, 2.14000000e+01],
       [4.48014500e+06, 2.00000000e+00, 2.00000000e-01, 9.88253103e+00,
        2.76532500e+01, 4.77130000e+04, 1.24780100e+02, 4.50000000e+00],
       [7.09380800e+06, 2.92000000e+00, 2.00000000e-01, 1.00011881e+01,
        2.71315100e+01, 2.85620000e+04, 1.21083800e+02, 4.90000000e+00],
       [5.93192340e+07, 1.39000000e+00, 3.00000000e-01, 7.46594241e+00,
        2.64802000e+01, 3.74750000e+04, 1.23703000e+02, 4.10000000e+00],
       [2.71734400e+06, 2.39000000e+00, 1.70000000e+00, 4.39145647e+00,
        2.40042100e+01, 8.95100000e+03, 1.25368500e+02, 1.89000000e+01],
       [1.27317900e+08, 1.34000000e+00, 6.00000000e-02, 9.53660569e+00,
        2.35000400e+01, 3.48000000e+04, 1.21965100e+02, 3.40000000e+00],
       [1.59159660e+07, 2.51000000e+00, 1.00000000e-01, 1.47181043e+01,
        2.62907800e+01, 1.87970000e+04, 1.28851700e+02, 2.59000000e+01],
       [3.82444420e+07, 4.76000000e+00, 6.30000000e+00, 2.66308378e-01,
        2.15925800e+01, 2.35800000e+03, 1.29934100e+02, 7.10000000e+01],
       [2.14421500e+06, 1.50000000e+00, 6.00000000e-01, 3.34184866e+00,
        2.64569300e+01, 2.09770000e+04, 1.29574600e+02, 1.05000000e+01],
       [4.10938900e+06, 1.57000000e+00, 1.00000000e-01, 3.99672180e+00,
        2.72011700e+01, 1.41580000e+04, 1.27503700e+02, 1.13000000e+01],
       [1.97219400e+06, 3.34000000e+00, 2.36000000e+01, 8.61766942e-03,
        2.19015700e+01, 2.04100000e+03, 1.31136100e+02, 1.14200000e+02],
       [3.67278200e+06, 5.19000000e+00, 1.60000000e+00, 1.57352183e-01,
        2.18953700e+01, 5.88000000e+02, 1.31255500e+02, 1.00900000e+02],
       [3.21980200e+06, 1.42000000e+00, 1.00000000e-01, 4.49848339e+00,
        2.68610200e+01, 2.32230000e+04, 1.30822600e+02, 8.20000000e+00],
       [4.85079000e+05, 1.63000000e+00, 3.00000000e-01, 2.21680797e+01,
        2.74340400e+01, 9.50010000e+04, 1.22370500e+02, 2.80000000e+00],
       [1.99267980e+07, 4.79000000e+00, 2.00000000e-01, 9.94221476e-02,
        2.14034700e+01, 1.52800000e+03, 1.32837100e+02, 6.67000000e+01],
       [1.39046710e+07, 5.78000000e+00, 1.12000000e+01, 8.24698808e-02,
        2.20346800e+01, 6.74000000e+02, 1.33939000e+02, 1.01100000e+02],
       [2.71974190e+07, 2.05000000e+00, 5.00000000e-01, 7.75223395e+00,
        2.47306900e+01, 1.99680000e+04, 1.23859300e+02, 8.00000000e+00],
       [3.21026000e+05, 2.38000000e+00, 6.00000000e-02, 3.27772577e+00,
        2.32199100e+01, 1.20290000e+04, 1.23322300e+02, 1.60000000e+01],
       [1.42234030e+07, 6.82000000e+00, 1.00000000e+00, 4.10788666e-02,
        2.17888100e+01, 1.60200000e+03, 1.28030800e+02, 1.48300000e+02],
       [4.06392000e+05, 1.38000000e+00, 1.00000000e-01, 6.18277102e+00,
        2.76836100e+01, 2.78720000e+04, 1.24157100e+02, 6.60000000e+00],
       [3.41455200e+06, 4.94000000e+00, 7.00000000e-01, 6.13103977e-01,
        2.26229500e+01, 3.35600000e+03, 1.29987500e+02, 1.03000000e+02],
       [1.23801300e+06, 1.58000000e+00, 9.00000000e-01, 3.07876290e+00,
        2.51566900e+01, 1.46150000e+04, 1.30878600e+02, 1.58000000e+01],
       [1.14972821e+08, 2.35000000e+00, 3.00000000e-01, 4.26117187e+00,
        2.74246800e+01, 1.58260000e+04, 1.22121600e+02, 1.79000000e+01],
       [4.11116800e+06, 1.49000000e+00, 4.00000000e-01, 1.31332119e+00,
        2.42369000e+01, 3.89000000e+03, 1.29942400e+02, 1.76000000e+01],
       [2.62966600e+06, 2.37000000e+00, 6.00000000e-02, 3.75948682e+00,
        2.48838500e+01, 7.56300000e+03, 1.29750400e+02, 3.48000000e+01],
       [3.13505440e+07, 2.44000000e+00, 1.00000000e-01, 1.59408314e+00,
        2.56318200e+01, 6.09100000e+03, 1.26528400e+02, 3.58000000e+01],
       [2.29948670e+07, 5.54000000e+00, 1.14000000e+01, 1.04748301e-01,
        2.19353600e+01, 8.64000000e+02, 1.35394900e+02, 1.14400000e+02],
       [5.10300060e+07, 2.05000000e+00, 6.00000000e-01, 1.91053400e-01,
        2.14493200e+01, 2.89100000e+03, 1.23142100e+02, 8.72000000e+01],
       [2.63251830e+07, 2.90000000e+00, 4.00000000e-01, 1.05412983e-01,
        2.07634400e+01, 1.86600000e+03, 1.25556100e+02, 5.07000000e+01],
       [1.65198620e+07, 1.77000000e+00, 2.00000000e-01, 1.05330281e+01,
        2.60154100e+01, 4.73880000e+04, 1.21695000e+02, 4.80000000e+00],
       [4.28538000e+06, 2.12000000e+00, 1.00000000e-01, 8.00908440e+00,
        2.77689300e+01, 3.21220000e+04, 1.18742100e+02, 6.40000000e+00],
       [5.59452400e+06, 2.72000000e+00, 2.00000000e-01, 7.78151613e-01,
        2.57729100e+01, 4.06000000e+03, 1.23479200e+02, 2.81000000e+01],
       [1.50851300e+07, 7.59000000e+00, 8.00000000e-01, 6.34371088e-02,
        2.12195800e+01, 8.43000000e+02, 1.35102100e+02, 1.41300000e+02],
       [1.51115683e+08, 6.02000000e+00, 3.60000000e+00, 6.14689662e-01,
        2.30332200e+01, 4.68400000e+03, 1.35492000e+02, 1.40900000e+02],
       [4.77163300e+06, 1.96000000e+00, 1.00000000e-01, 1.05297688e+01,
        2.69342400e+01, 6.52160000e+04, 1.26026600e+02, 3.60000000e+00],
       [2.65228100e+06, 2.89000000e+00, 1.00000000e-01, 1.55720805e+01,
        2.62410900e+01, 4.77990000e+04, 1.26887000e+02, 1.19000000e+01],
       [1.63096985e+08, 3.58000000e+00, 1.00000000e-01, 9.35618056e-01,
        2.22991400e+01, 4.18700000e+03, 1.26519600e+02, 9.55000000e+01],
       [3.49867900e+06, 2.61000000e+00, 9.00000000e-01, 2.22379634e+00,
        2.62695900e+01, 1.40330000e+04, 1.22682900e+02, 2.10000000e+01],
       [6.54026700e+06, 4.07000000e+00, 9.00000000e-01, 5.30746337e-01,
        2.50150600e+01, 1.98200000e+03, 1.20052400e+02, 6.97000000e+01],
       [6.04713100e+06, 3.06000000e+00, 3.00000000e-01, 6.98581746e-01,
        2.55422300e+01, 6.68400000e+03, 1.23615000e+02, 2.57000000e+01],
       [2.86420480e+07, 2.58000000e+00, 4.00000000e-01, 1.45013444e+00,
        2.47704100e+01, 9.24900000e+03, 1.19636800e+02, 2.32000000e+01],
       [9.02971150e+07, 3.26000000e+00, 6.00000000e-02, 8.42120697e-01,
        2.28726300e+01, 5.33200000e+03, 1.22345900e+02, 3.34000000e+01],
       [3.85257520e+07, 1.33000000e+00, 1.00000000e-01, 8.27076715e+00,
        2.66738000e+01, 1.99960000e+04, 1.29676500e+02, 6.70000000e+00],
       [1.05774580e+07, 1.36000000e+00, 5.00000000e-01, 5.48692640e+00,
        2.66844500e+01, 2.77470000e+04, 1.27263100e+02, 4.10000000e+00],
       [1.38896200e+06, 2.20000000e+00, 6.00000000e-02, 4.87020615e+01,
        2.81313800e+01, 1.26076000e+05, 1.26315300e+02, 9.50000000e+00],
       [2.07416690e+07, 1.34000000e+00, 1.00000000e-01, 4.38344907e+00,
        2.54106900e+01, 1.80320000e+04, 1.28755300e+02, 1.61000000e+01],
       [1.43123163e+08, 1.49000000e+00, 1.00000000e+00, 1.19827176e+01,
        2.60113100e+01, 2.25060000e+04, 1.28490300e+02, 1.35000000e+01],
       [9.75031400e+06, 5.06000000e+00, 2.90000000e+00, 5.42444698e-02,
        2.25545300e+01, 1.17300000e+03, 1.35100500e+02, 7.83000000e+01],
       [1.22297030e+07, 5.11000000e+00, 8.00000000e-01, 4.61633711e-01,
        2.19274300e+01, 2.16200000e+03, 1.30279500e+02, 7.58000000e+01],
       [9.10953500e+06, 1.41000000e+00, 1.00000000e-01, 5.27122268e+00,
        2.65149500e+01, 1.25220000e+04, 1.30375500e+02, 8.00000000e+00],
       [5.52183800e+06, 5.13000000e+00, 1.60000000e+00, 1.18255775e-01,
        2.25313900e+01, 1.28900000e+03, 1.34716000e+02, 1.79100000e+02],
       [4.84964100e+06, 1.28000000e+00, 1.00000000e-01, 4.11444075e+00,
        2.38399600e+01, 6.59910000e+04, 1.21173600e+02, 2.80000000e+00],
       [5.39671000e+06, 1.31000000e+00, 6.00000000e-02, 6.90165446e+00,
        2.69271700e+01, 2.46700000e+04, 1.29528000e+02, 8.80000000e+00],
       [2.03059900e+06, 1.43000000e+00, 6.00000000e-02, 8.51182820e+00,
        2.74398300e+01, 3.08160000e+04, 1.29923100e+02, 3.70000000e+00],
       [9.13258900e+06, 7.06000000e+00, 6.00000000e-01, 6.82188892e-02,
        2.19691700e+01, 6.15000000e+02, 1.31531800e+02, 1.68500000e+02],
       [5.03488110e+07, 2.54000000e+00, 1.79000000e+01, 9.42796037e+00,
        2.68553800e+01, 1.22630000e+04, 1.30994900e+02, 6.61000000e+01],
       [4.58170160e+07, 1.42000000e+00, 4.00000000e-01, 7.29308876e+00,
        2.74997500e+01, 3.46760000e+04, 1.22045300e+02, 5.00000000e+00],
       [1.99495530e+07, 2.32000000e+00, 6.00000000e-02, 5.80791088e-01,
        2.19667100e+01, 6.90700000e+03, 1.24861500e+02, 1.17000000e+01],
       [3.44701380e+07, 4.79000000e+00, 1.00000000e+00, 3.82117945e-01,
        2.24048400e+01, 3.24600000e+03, 1.29719900e+02, 8.47000000e+01],
       [5.06657000e+05, 2.41000000e+00, 1.00000000e+00, 4.74113997e+00,
        2.54988700e+01, 1.34700000e+04, 1.24635800e+02, 2.64000000e+01],
       [1.15375000e+06, 3.70000000e+00, 2.59000000e+01, 9.49860795e-01,
        2.31696900e+01, 5.88700000e+03, 1.31879300e+02, 1.12200000e+02],
       [9.22633300e+06, 1.92000000e+00, 1.00000000e-01, 5.31568840e+00,
        2.63762900e+01, 4.34210000e+04, 1.22947300e+02, 3.20000000e+00],
       [7.64654200e+06, 1.47000000e+00, 4.00000000e-01, 5.33305762e+00,
        2.62019500e+01, 5.50200000e+04, 1.19646500e+02, 4.70000000e+00],
       [7.25407200e+06, 3.70000000e+00, 2.00000000e-01, 4.53167660e-01,
        2.37796600e+01, 2.00100000e+03, 1.29965700e+02, 5.62000000e+01],
       [4.28447440e+07, 5.54000000e+00, 5.80000000e+00, 1.54672995e-01,
        2.24779200e+01, 2.03000000e+03, 1.30832800e+02, 7.24000000e+01],
       [6.64532550e+07, 1.48000000e+00, 1.30000000e+00, 3.83510189e+00,
        2.30080300e+01, 1.22160000e+04, 1.20496900e+02, 1.56000000e+01],
       [6.05293700e+06, 4.88000000e+00, 3.20000000e+00, 2.51983337e-01,
        2.18787500e+01, 1.21900000e+03, 1.31024800e+02, 9.64000000e+01],
       [1.31537200e+06, 1.80000000e+00, 1.50000000e+00, 3.19577173e+01,
        2.63966900e+01, 3.08750000e+04, 1.24993900e+02, 2.49000000e+01],
       [1.04080910e+07, 2.04000000e+00, 6.00000000e-02, 2.44066948e+00,
        2.51569900e+01, 9.93800000e+03, 1.28629100e+02, 1.94000000e+01],
       [7.03443570e+07, 2.15000000e+00, 6.00000000e-02, 4.02190259e+00,
        2.67037100e+01, 1.64540000e+04, 1.24067500e+02, 2.22000000e+01],
       [3.10144270e+07, 6.34000000e+00, 6.40000000e+00, 1.00852839e-01,
        2.23583300e+01, 1.43700000e+03, 1.34520400e+02, 8.93000000e+01],
       [4.60284760e+07, 1.38000000e+00, 1.10000000e+00, 7.03235908e+00,
        2.54237900e+01, 8.76200000e+03, 1.31496200e+02, 1.29000000e+01],
       [6.16896200e+07, 1.87000000e+00, 2.00000000e-01, 8.52646682e+00,
        2.73924900e+01, 3.77390000e+04, 1.24084500e+02, 5.60000000e+00],
       [3.04473143e+08, 2.07000000e+00, 6.00000000e-01, 1.85459917e+01,
        2.84569800e+01, 5.03840000e+04, 1.18477700e+02, 7.70000000e+00],
       [3.35083200e+06, 2.11000000e+00, 5.00000000e-01, 2.48976355e+00,
        2.63912300e+01, 1.53170000e+04, 1.24260400e+02, 1.30000000e+01],
       [2.69527190e+07, 2.46000000e+00, 1.00000000e-01, 4.47666902e+00,
        2.53205400e+01, 3.73300000e+03, 1.24346200e+02, 4.92000000e+01],
       [8.65893420e+07, 1.86000000e+00, 4.00000000e-01, 1.47934658e+00,
        2.09163000e+01, 4.08500000e+03, 1.21936700e+02, 2.62000000e+01],
       [1.31145790e+07, 5.88000000e+00, 1.36000000e+01, 1.48981514e-01,
        2.06832100e+01, 3.03900000e+03, 1.32449300e+02, 9.49000000e+01],
       [1.34954620e+07, 3.85000000e+00, 1.51000000e+01, 6.54323190e-01,
        2.20266000e+01, 1.28600000e+03, 1.31974500e+02, 9.83000000e+01]])

X_gapminder = pd.read_csv("datasets/X_gapminder.csv").values
X_gapminder[:5]

array([[3.48110590e+07, 2.73000000e+00, 1.00000000e-01, 3.32894466e+00,
        2.45962000e+01, 1.23140000e+04, 1.29904900e+02, 2.95000000e+01],
       [1.98422510e+07, 6.43000000e+00, 2.00000000e+00, 1.47435339e+00,
        2.22508300e+01, 7.10300000e+03, 1.30124700e+02, 1.92000000e+02],
       [4.03818600e+07, 2.24000000e+00, 5.00000000e-01, 4.78516998e+00,
        2.75017000e+01, 1.46460000e+04, 1.18891500e+02, 1.54000000e+01],
       [2.97502900e+06, 1.40000000e+00, 1.00000000e-01, 1.80410622e+00,
        2.53554200e+01, 7.38300000e+03, 1.32810800e+02, 2.00000000e+01],
       [2.13703480e+07, 1.96000000e+00, 1.00000000e-01, 1.80163133e+01,
        2.75637300e+01, 4.13120000e+04, 1.17375500e+02, 5.20000000e+00]])

y_gapminder = np.array([75.3, 58.3, 75.5, 72.5, 81.5, 80.4, 70.6, 72.2, 68.4, 75.3, 70.1,
       79.4, 70.7, 63.2, 67.6, 70.9, 61.2, 73.9, 73.2, 59.4, 57.4, 66.2,
       56.6, 80.7, 54.8, 78.9, 75.1, 62.6, 58.6, 79.7, 55.9, 76.5, 77.8,
       78.7, 61. , 74. , 70.1, 74.1, 56.7, 60.4, 74. , 65.7, 79.4, 81. ,
       57.5, 62.2, 72.1, 80. , 62.7, 79.5, 70.8, 58.3, 51.3, 63. , 61.7,
       70.9, 73.8, 82. , 64.4, 69.5, 76.9, 79.4, 80.9, 81.4, 75.5, 82.6,
       66.1, 61.5, 72.3, 77.6, 45.2, 61. , 72. , 80.7, 63.4, 51.4, 74.5,
       78.2, 55.8, 81.4, 63.6, 72.1, 75.7, 69.6, 63.2, 73.3, 55. , 60.8,
       68.6, 80.3, 80.2, 75.2, 59.7, 58. , 80.7, 74.6, 64.1, 77.1, 58.2,
       73.6, 76.8, 69.4, 75.3, 79.2, 80.4, 73.4, 67.6, 62.2, 64.3, 76.4,
       55.9, 80.9, 74.8, 78.5, 56.7, 55. , 81.1, 74.3, 67.4, 69.1, 46.1,
       81.1, 81.9, 69.5, 59.7, 74.1, 60. , 71.3, 76.5, 75.1, 57.2, 68.2,
       79.5, 78.2, 76. , 68.7, 75.4, 52. , 49. ])

y_gapminder = pd.read_csv("datasets/y_gapminder.csv").values
y_gapminder[:5]

array([[75.3],
       [58.3],
       [75.5],
       [72.5],
       [81.5]])

# Setup the pipeline steps: steps
steps_gapminder = [('imputation', SimpleImputer(missing_values=np.nan, strategy="mean")),
         ("scaler", StandardScaler()),
         ("elasticnet", ElasticNet())]

# Create the pipeline: pipeline 
pipeline_gapminder = Pipeline(steps_gapminder)

# Specify the hyperparameter space
parameters_gapminder = {"elasticnet__l1_ratio":np.linspace(0,1,30)}

# Create train and test sets
X_train_gapminder, X_test_gapminder, y_train_gapminder, y_test_gapminder = train_test_split(X_gapminder, 
                                                                                            y_gapminder, 
                                                                                            test_size=.4, 
                                                                                            random_state=42)

# Create the GridSearchCV object: gm_cv
gm_cv_gapminder = GridSearchCV(pipeline_gapminder, param_grid=parameters_gapminder, cv=3)

# Fit to the training set
gm_cv_gapminder.fit(X_train_gapminder, y_train_gapminder)

# Compute and print the metrics
r2_gapminder = gm_cv_gapminder.score(X_test_gapminder, y_test_gapminder)
print("Tuned ElasticNet Alpha: {}".format(gm_cv_gapminder.best_params_))
print("Tuned ElasticNet R squared: {}".format(r2_gapminder))

Tuned ElasticNet Alpha: {'elasticnet__l1_ratio': 1.0}
Tuned ElasticNet R squared: 0.8862016570888216